Tasks by the Pythagorean theorem. Independent work "problems on the topic" Pythagorean theorem "
MBNOU "Lyceum No. 3 (arts)"
The lesson was prepared by the math teacher
Elena Svatkovskaya
OPEN LESSON ON GEOMETRY
"SOLUTION OF PROBLEMS ON THE TOPIC" PYTHAGOR'S THEOREM "
Lesson type: lesson - generalization.Lesson objectives: A) educational: ensuring a solid and conscious mastery of the system of geometric knowledge and skills necessary in everyday life and work, sufficient for the study of related disciplines and continuing education; the formation of algorithmic thinking; the formation of interest in the subject; B) developing: develop students' accurate, economical, informative speech, the ability to select the most appropriate language (in particular, symbolic, graphic) means; creative thinking activity of students in the classroom by solving problems with an unformulated question, data analysis, research tasks; to contribute to the development of the intellectual qualities of the personality of schoolchildren (independence, flexibility of thinking, the ability to "see" the problem, evaluative actions, generalization), fast switching; the ability to develop skills for individual and independent work; to form the ability to express thoughts clearly and clearly; the use of the Pythagorean theorem, the corollary and its inverse theorem for the formation of skills: finding an unknown leg or hypotenuse from a right-angled triangle or elements of other figures, to determine the type of triangle. C) educational: to educate the ability to act according to a given algorithm and design new ones; to give a general acquaintance with the methods of cognition of reality; understanding the beauty and grace of mathematical reasoning; instill in students an interest in the subject by including them in solving practical problems, using information technologies; to form the ability to clearly and competently perform mathematical notes.
Develop COMPETENCIES:
Responsibility and adaptability Communication skills Creativity and curiosity Critical and systemic thinking Ability to work with information and media Ability to pose and solve problems Focus on self-development Social responsibility
ICT: use in the lesson of presentation and computer testing.
LESSON PLAN:
- Repetition of the passed material. (slides 1-4) Homework check: Indian mathematician Bhaskara's poplar problem. (slide 5-6) Oral survey. (slides 7-13) Verification of the passed material in the form of testing, followed by verification by the students themselves. (slides 14-17) Solving problems on the topic "Pythagorean Theorem":
- Homework: (slides 26-29)
- Historical background (slides 30-34). Summing up the results of the lesson, assigning marks.
DURING THE CLASSES:
1. REPEAT KNOWLEDGE.
Slides 1-4 with theoretical calculations are projected onto the board.
2. CHECKING HOME WORK.
Slides 5-6 are projected onto the board. Students check the correctness of the implementation problems about the poplar of the Indian mathematician Bhaskara.
A lonely poplar grew on the bank of the river. Suddenly a gust of wind broke his trunk. The poor poplar fell. And the angle of a straight line with the flow of the river was its trunk. Now remember that at that point the river was only four feet wide. The top bent at the edge of the river, leaving only three feet of the trunk. I beg you, now tell me soon: how great is the height of the poplar?
Solution.Let CD be the height of the barrel.BD = ABBy the Pythagorean theorem, we haveAB² = AC² + BC²,AB² = 9 + 16 = 25, AB = 5.CD = CB + BD,CD = 3 + 5 = 8.Answer: 8 feet.

So, the KOV triangle is rectangular: AB = 2AK = 2KV; OV = OK + KV OV = OK + KV OV = 12 + 5 = 144 + 25 = 169 KV = OV-KO = 17-8 = 289-64 = 225 ОВ = 13 (cm). CV = 15 (cm) AB = 2KV = 30 (cm).
6. HOME TASK.
Students receive a printout of the problem texts.
a) An old problem from the Chinese "Mathematics in nine books": 
"There is a reservoir with a side of 1 zhang = 10 chi. In the center of it there is a reed that protrudes 1 chi above the water. If you pull the reed to the shore, it will just touch it. The question is: what is the depth of the water and what is the length of the reeds? "
b) Problem using the properties of the tangent to the circle:
A tangent MC is drawn to a circle with center O, where M is a tangent point.
Find:
a) MK, if OK = 12 m, and the radius of the circle is 8 mm;
b) the radius of the circle, if MK = 6 cm, OK = 8 cm.
c) Parsing the memo.
d) Solve the crossword puzzle:

- One of the sides of a right-angled triangle; The action used in the Pythagorean theorem; Side of a right-angled triangle opposite to a right angle; Ancient Greek mathematician, whose name is given to the theorem studied in the lesson; The figure referred to in the Pythagorean theorem; The type of triangle for which the statement "The square of the hypotenuse is equal to the sum of the squares of the legs" is true; The degree to which both the hypotenuse and legs are raised in the Pythagorean theorem.
7. HISTORICAL REFERENCE.
Slides 29-33 are shown on the board with information about the birth of Pythagoras, the discovery of the Pythagorean theorem. Students who have prepared the material in advance will read the passages.
a) Pythagoras was born somewhere between 600 and 590. before the birth of Christ and lived for about a hundred years. Many strange legends have survived to this day about his birth. Some of them argue that he was not an ordinary mortal man, but was one of the gods who took on human form in order to enter the world and teach humanity.

b) For 1000 years of ancient tradition, real and deeply respectful information for the personality of Pythagoras was mixed with many legends, fairy tales and fables. Legends vied with each other to proclaim Pythagoras a miracle worker; it was reported that he had a golden thigh, that people saw him at the same time in two different cities talking with his disciples, that once, when he crossed the river with numerous companions and spoke to it, the river overflowed its banks and in a loud superhuman voice exclaimed: “Yes Hello Pythagoras! ”that in Tyrrenia he killed with his bite a poisonous snake that took the lives of many Tyrrhenians, that he predicted earthquakes, stopped general diseases, ward off hurricanes, and tamed sea waves.
c) Porfiry tells the following story about Pythagoras: in “Tarentum, he saw a bull on herbs, chewing green beans, went up to the shepherd and advised him to tell the bull not to do this. The shepherd began to laugh and said that he could not speak bullish; then Pythagoras himself went up to the bull and whispered something in his ear, after which he not only immediately went away from the bean but never touched the beans again, but lived since then and died in old age in Tarentum at the temple of Hera , where he was known as a sacred bull and fed on bread, which was given to him by passers-by. "
d) Diogenes Laertius, for example, says: “Having appeared in Italy, Pythagoras made himself a dwelling underground, and ordered his mother to write down everything that happened and when on the tablets, and put the plates down to him until he came out. Mother did so; and Pythagoras, after waiting for the time, went out, withered like a skeleton, appeared before the assembly of the people and declared that he had come from Hades, and at the same time read to them about everything that happened to them. Everyone was shocked by what they read, wept and sobbed, and Pythagoras was considered God. And nevertheless, the basic tone of all the legends about Pythagoras was the same:
"They don't talk about anyone so much and so extraordinary" (Porfiry).
e) The discovery of the theorem by Pythagoras is surrounded by a halo of beautiful legends. Proclus, commenting on the last sentence of the first book of the "Elements" of Euclid, writes: “If you listen to those who like to repeat ancient legends, then you will have to say that this theorem goes back to Pythagoras; they say that in honor of this discovery he sacrificed a bull. " However, more generous storytellers turned one bull into one hecatomb, and this is already a whole hundred. And although even Cicero noticed that any shedding of blood was alien to the charter of the Pythagorean order, this legend was firmly merged with the Pythagorean theorem and, two thousand years later, continued to evoke warm responses.
8. SUMMARIZING THE LESSON.
Find the height lowered to the hypotenuse of a right triangle if its legs are 3 cm and 5 cm.
In order to solve this problem, it is necessary to draw a triangle, and certainly a rectangular one. For the convenience of further solution, I will draw it lying on the hypotenuse.
Now let's draw the height. What is this anyway? This is a line dropped from the corner of the triangle to the opposite side, and forms a right angle with this side. 
Where did the root figure of 34 cm come from? It is very easy to find the hypotenuse of a triangle with known legs according to the Pythagorean theorem: (square of one leg) + (square of the second leg) = (square of the hypotenuse) = 9 + 25 = 34.
Hypotenuse = root of the square of the hypotenuse = root of 34 cm.
After holding the height, two inner triangles appeared. In our task, in fact, the designation with letters is useless, but for clarity: 
So, there was a triangle ABC, in it the height BD was lowered to the hypotenuse AC. It turned out two inner right-angled triangles: ADB and BDC. We do not know how the height divided the hypotenuse, so we denote the smaller unknown part - AD - through x, and the larger - DC - through the difference between AC and x, i.e. (root of 34) -x cm. 
Let's denote the required height through y. Now, according to the Pythagorean theorem, from two inner right-angled triangles we compose a system of equations:
x ^ 2 + y ^ 2 = 9
((root of 34) -x) ^ 2 + y ^ 2 = 25
Express y ^ 2 from the first equation: y ^ 2 = 9 - x ^ 2
Substituting, simplifying the second equation in advance: ((root of 34) -x) ^ 2 + y ^ 2 = 34 - 2 * (root of 34) * x + x ^ 2 + y ^ 2 = 34 - 2 * (root of 34) * x + x ^ 2 + 9 - x ^ 2 = 43 - 2 * (root of 34) * x = 25
2 * (root of 34) * x = 18
x = 9 / (root of 34)
Hooray! Almost done! Now again, by the Pythagorean theorem, from the triangle ABD:
(square of hypotenuse) - ((found x) squared) = square of desired height
AB ^ 2 - x ^ 2 = 9 - 81/34 = 225/34 = h ^ 2
h = 15 / (root of 34)
When you first started learning square roots and how to solve irrational equations (equalities containing an unknown under the root sign), you probably got your first idea of their practical use. The ability to extract the square root of numbers is also necessary for solving problems on the application of the Pythagorean theorem. This theorem connects the lengths of the sides of any right triangle.
Let the lengths of the legs of a right-angled triangle (those two sides that converge at right angles) be denoted by letters and, and the length of the hypotenuse (the longest side of the triangle opposite the right angle) be denoted by a letter. Then the corresponding lengths are related by the following relation:
This equation allows you to find the length of the side of a right-angled triangle in the case when the length of its other two sides is known. In addition, it allows you to determine whether the triangle in question is right-angled, provided that the lengths of all three sides are known in advance.
Solving problems using the Pythagorean theorem
To consolidate the material, we will solve the following problems on the application of the Pythagorean theorem.

So, given:
- The length of one of the legs is 48, the hypotenuse is 80.
- The length of the leg is 84, the hypotenuse is 91.
Let's start solving:
a) Substitution of data into the above equation gives the following results:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 or b = -64
Since the side length of a triangle cannot be expressed as a negative number, the second option is automatically discarded.
Answer to the first figure: b = 64.
b) The length of the leg of the second triangle is found in the same way:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 or b = -35
As in the previous case, the negative decision is discarded.
Answer to the second figure: b = 35

We are given:
- The lengths of the smaller sides of the triangle are 45 and 55, respectively, and the larger ones are 75.
- The lengths of the smaller sides of the triangle are 28 and 45, respectively, and the larger ones are 53.
We solve the problem:
a) It is necessary to check whether the sum of the squares of the lengths of the smaller sides of the given triangle is equal to the square of the length of the larger one:
45 2 + 55 2 = 2025 + 3025 = 5050
Therefore, the first triangle is not right-angled.
b) The same operation is performed:
28 2 + 45 2 = 784 + 2025 = 2809
Therefore, the second triangle is right-angled.
First, find the length of the largest segment formed by the points with coordinates (-2, -3) and (5, -2). To do this, we use the well-known formula for finding the distance between points in a rectangular coordinate system:
Similarly, we find the length of the segment enclosed between the points with coordinates (-2, -3) and (2, 1):
Finally, we determine the length of the segment between the points with coordinates (2, 1) and (5, -2):
Since the equality holds:
then the corresponding triangle is right-angled.
Thus, we can formulate the answer to the problem: since the sum of the squares of the sides with the shortest length is equal to the square of the side with the greatest length, the points are the vertices of a right-angled triangle.
The base (located strictly horizontally), the jamb (located strictly vertically) and the cable (extended diagonally) form a right-angled triangle, respectively, the Pythagorean theorem can be used to find the length of the cable:
Thus, the length of the cable will be approximately 3.6 meters.
Given: the distance from point R to point P (leg of the triangle) is 24, from point R to point Q (hypotenuse) - 26.
So, we help Vitya solve the problem. Since the sides of the triangle shown in the figure are supposed to form a right-angled triangle, the Pythagorean theorem can be used to find the length of the third side:
So, the width of the pond is 10 meters.
Sergey Valerievich
As a symbol of eternal union
As an eternal friendship is a simple sign
You connected, hypotenuse,
Forever legs with you.
You hid a secret
Some wise Greek did not appear soon
And the Pythagorean theorem
He glorified you forever.
Goals:
- systematize, generalize knowledge and skills on the application of the Pythagorean theorem in solving problems, show their practical application;
- promote the development of mathematical thinking;
- cultivate cognitive interest.
Equipment: portrait of Pythagoras, drawing and layout of a television tower, tables for oral counting.
DURING THE CLASSES
1. Organizational moment
2. Work on finished drawings
- Is it possible to find the area of a triangle using these conditions?
- What other question can be asked about these tasks?
- Find the areas of the triangles.
- What theorem did you use to find the sides of triangles?
- What are the names of triangles 1, 4 and 3? (Pythagorean)
- Give more examples of such triangles.
- Is it a right-angled triangle with sides 6, 29 and 25? Which theorem did you use to prove?
At this time, 4 students work independently.
1. Find the area of a rectangle if its diagonal is 10 cm and forms an angle of 30 ° with the side. (25√3 cm 2)
2. In a rectangular trapezoid, the bases are 22 cm and 6 cm, the large side side is 20 cm. Find the area of the trapezoid. (224 cm 2)
3. Independent work of 3 levels according to ready-made drawings.
Option 1
| 1) a = 3 cm |
2) s = 10 cm |
3) a = 10 cm |
|
||
Option 2
1)
|
2)
|
3)
|
Option 3
Self-test of works using the answer table.
4. Solving problems
Find the side and area of the rhombus if its diagonals are 10 cm and 24 cm.

Given: ABCD - rhombus, BD = 10 cm, AC = 24 cm
Find: AB and S rhombus
1. ВD is perpendicular to АС according to the property of rhombus diagonals.
2. Consider a triangle ABO: O = 90, BO = 5 cm, AO = 12 cm. By the Pythagorean theorem AB = BO 2 + AO 2 AB = 13 cm
3.S = 1/2 * 10 * 24 = 120 cm 2.
Answer: AB = 13 cm, S = 120 cm 2
Find the area of the trapezoid ABCD with bases AB and CD if AB = 10 cm, BC = DA = 13 cm, CD = 20 cm.
Given: ABCD - trapezoid, AB and CD bases, AB = 10
СD = 20 cm, ВС = DA = 13 cm
Find: S?

1. Let's draw the height АН and consider the triangle АDН: Н = 90, АD = 13 cm,
DН = (20 - 10): 2 = 5 cm.
AH = 13 2 - 5 2 = 12 cm
2.S = (20 + 10): 2 * 12 = 180 cm 2
Answer: S = 180cm 2.
- What formulas did you use when solving problems? What formulas for calculating the area of a triangle do you know?
Today Masha L. will introduce you to the formula for calculating the area of an equilateral triangle along its side. (The student prepared the task at home on her own.)
S = a 2 * √3 / 4, where a is the side of the triangle.
Solution of the problem for the application of this formula.
The triangle consists of 4 triangles with a side of 1cm. How many equilateral triangles do you see? What is the area of this triangle?
Solution to the problem: 5 equilateral triangles, a = 2 cm, then S = √3 square units.

5. Practical task
Pupils' report on the work done: In our village there is a TV tower, the height of which is 124 m. In order for it to stand upright, stretchers are required, they are several level. We were given the task of finding out how many meters of cable will be required for the 4 lower guy lines.

Since the braces are of the same length, the task was reduced to finding the length of one stretch. To do this, we have selected a right-angled triangle, the legs of which are the distances AC and CB. We learned that the cable is attached at a height of 40 m (AC = 40 m) and measured the distance from the base of the tower to the cable attachment on the surface (CB = 24 m). According to the Pythagorean theorem, AB = 46.7 m, which means that the cable will need at least 186.8 m.
During the report, the model of the TV tower and its drawing are demonstrated.
6. Lesson summary
7. Homework
End the lesson with these words: It is said that science is different from art in that while the creations of art are eternal, the great creations of science are hopelessly aging. Fortunately, this is not so, the Pythagorean theorem is an example of this, we have applied and will apply it in solving problems.
Lesson topic
Pythagorean theorem
Lesson objectives
Get to know schoolchildren with the Pythagorean theorem;
Formulate and prove the Pythagorean theorem;
To acquaint schoolchildren with different methods of applying this theorem when solving problems;
To form the skills of using the acquired knowledge in practice;
Develop student attention, independence and interest in geometry;
To foster a culture of mathematical speech.
Lesson Objectives
Learn to use the properties of shapes when completing assignments.
Be able to apply the Pythagorean theorem while solving problems.
Lesson plan
Brief biographical information.
Theorem and its proof.
Interesting Facts.
Solving problems.
Homework.
Brief biographical information about Pythagoras
Unfortunately, Pythagoras did not leave any writings about his biography, so we can learn all the information about this great philosopher and famous mathematician only thanks to the memoirs of his followers, and even then not always fair. Therefore, there are many legends about this man. But the truth is that Pythagoras was a great Hellenic sage, philosopher and talented mathematician.
According to inaccurate information, the great sage and brilliant scientist Pythagoras was born into a far from poor family, on the island of Samoseya, about 570 BC.
The birth of a brilliant child was predicted by Pafia. Therefore, the future luminary received its name Pythagoras, which means that this is the one that Paphia announced. She predicted that a born baby in the future will bring many benefits and goodness to people.
The newborn was insanely beautiful, and in modern times he delighted those around him with his outstanding abilities. And since the young talent whiled away his days among the wise elders, in the future it bore fruit. This is how, thanks to Hermodamantus, Pythagoras fell in love with music, and Ferekid directed the child's mind to the Logos. After living in Samoseya, Pythagoras went to Mileet, where he met another scientist - Thales.
Pythagoras got acquainted with the knowledge of all the sages known at that time, since he was allowed to study and learn all the mysteries that were forbidden to others. He tried to get to the bottom of the truth and absorb all the knowledge accumulated by mankind.
After twenty-two years in Egypt, Pythagoras moved to Babylon, where he continued his communication with various sages and magicians. Returning to Samios at the end of his life, he was recognized as one of the wisest people of that time.
Pythagorean theorem

Even a person who has not yet had a chance to study this theorem must have heard the saying about "Pythagorean pants." The peculiarity of this theorem is that it has become one of the key theorems in Euclidean geometry. It allows you to easily find and establish a correspondence between the sides of a right-angled triangle.
The Pythagorean theorem was remembered by every schoolchild not only for the statement: "Pythagorean pants are equal on all sides," but for its simplicity and significance. And at first glance, this theorem, although it seems simple, is of great importance, since in geometry it is applied practically at every step.
The Pythagorean theorem has a large number of different proofs and is probably the only theorem that has such a huge number of proofs. This diversity underlines the boundless significance of this theorem.
The Pythagorean theorem contains geometric, algebraic, mechanical and other proofs.
There are many different legends about the discovery of the theorem by Pythagoras. But, despite all this, the name of Pythagoras entered the history of geometry forever and firmly merged with the Pythagorean theorem. After all, this brilliant mathematician will be the first to present the proof of the theorem that bears his name.

Theorem statement
There are several formulations of the Pythagorean theorem.
Euclidean theorem tells us that the square of the side of a right-angled triangle, drawn over its right angle, is equal to the squares on the sides that enclose the right angle.

Assignment: Find different formulations of the Pythagorean theorem. Do you find any difference in them?
Simplified proof of Euclid
Regardless of whether we take the decomposition method or Euclid's proof, you can use any arrangement of the squares. In some cases, small simplifications can be achieved.

Take a square, which is built on one of the legs and has the same location as the triangle. We see that the extension of the side opposite to the leg of this square passes through the apex of the square, which is built on the hypotenuse.
The proof of the theorem looks quite simple, since it will be enough to simply compare the areas of figures with the area of a triangle. And we see that S of a triangle is equal to ½ the area of a square, and also ½ S of a rectangle.
The simplest proof

Algebraic proof
The algebraic proof of the Pythagorean theorem includes elementary methods that are present in algebra. These are ways to solve equations combined with a way to change variables.
Let's take a closer look at this proof. And so, we have a rectangle ABC, whose right angle is C.
Draw the height of the CD from this corner.
According to the definition of the cosine of the angle, we get:
cosA = AD / AC = AC / AB. Hence AB * AD = AC2.
And correspondingly:
cosB = BD / BC = BC / AB.
Hence AB * BD = BC2.
Now we add these equalities term by term and see that: AD + DB = AB,
AC2 + BC2 = AB (AD + DB) = AB2.
That's all, the theorem is proven.

Scientists "proved" the Pythagorean theorem with the help of cartoons. A group of like-minded people from the Institute. Steklova received an award for an original mathematical project that they developed for schoolchildren and teachers. They created mini math lessons that turned this boring subject into a very interesting and informative one. Young scientists released their unusual sketches on disks and posted them on the Internet for everyone to see.
Questions
1. Who is Pythagoras?
2. What does the Pythagorean theorem say?
3. What formulations of the Pythagorean theorem exist?
4. When solving what problems the Pythagorean theorem is applied?
5. Where did the Pythagorean theorem find practical application?
6. What ways do you know of using the Pythagorean theorem?
Problems using the Pythagorean theorem

Using your knowledge of the Pythagorean theorem, try to solve the following problems:
At the same time, two groups of tourists left the tourist base. The first group went south and walked seven kilometers, and the second turned west and walked nine kilometers. Using the knowledge of the theorem, find the distance between the groups of tourists.
If in a right-angled triangle its leg is 15 cm, and the hypotenuse is 16 cm, then what will the second leg be equal to?
What will be the area of the trapezoid when its large base is 24 cm, the smaller one is 16, and the large diagonal of the rectangular trapezoid is 26 cm?

Homework
Draw up in the form of a short report several proofs of the Pythagorean theorem that you understand and solve the problems.
1. Find the diagonal of a right-angled triangle, provided that its sides are 8 cm and 32 cm.
2. Find the median of the triangle, which is drawn to the base, if the perimeter of an isosceles triangle is 38 cm, and its lateral side is 15 cm.
3. A triangle has sides 10cm, 6cm and 9cm. Try to determine if this triangle is right-angled?

 (cos
(cos  (AC² = AO² + OS²) c) What are the names of right-angled triangles, whose sides are integers numbers?(Pythagorean)
(AC² = AO² + OS²) c) What are the names of right-angled triangles, whose sides are integers numbers?(Pythagorean) 

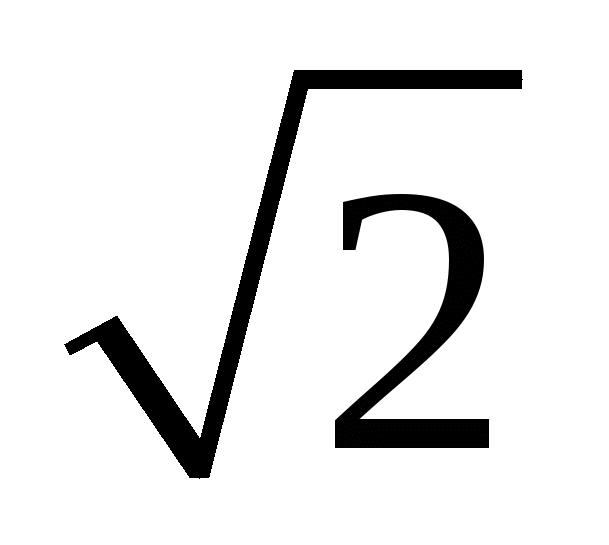 e) 2a
e) 2a 
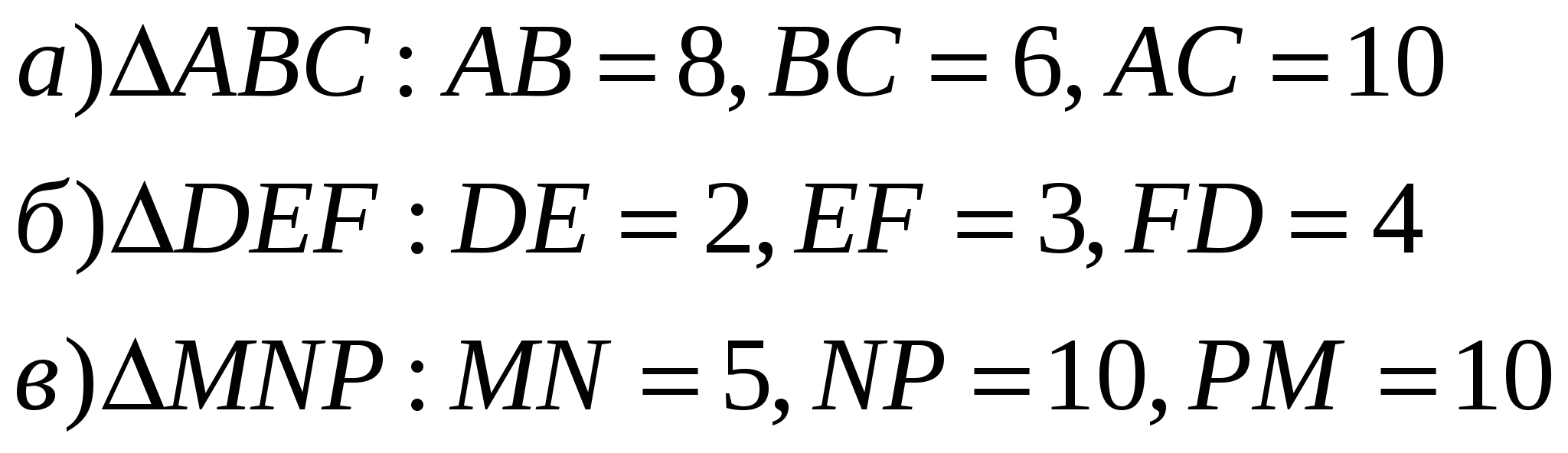
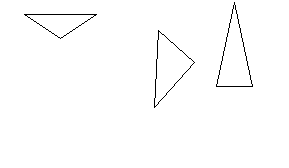 a B C)
a B C) 
 (m)
(m)


