Domain and range of values ​​of the function. In elementary mathematics, functions are studied only on the set of real numbers R This means that the argument of a function can only take valid values ​​for which the function is defined, i.e. it also only takes valid values. Lots of X all valid valid argument values x for which the function y= f(x) is defined, called function scope... Lots of Y all valid values y that the function takes is called function range... Now we can give a more precise definition of the function: the rule(law of) correspondence between sets X and Y, according to which for each element of the setX you can find one and only one element from the set Y, called the function.

It follows from this definition that a function is considered given if:

The scope of the function is specified X ;

The range of values ​​of the function is set Y ;

The rule (law) of correspondence is known, and such that for each

Argument values ​​can only be found one function value.

This requirement for unambiguous functions is mandatory.

Monotonic function. If for any two values ​​of the argument x 1 and x 2 from condition x 2 > x 1 follows f(x 2) > f(x 1), then the function f(x) is called increasing; if for any x 1 and x 2 from condition x 2 > x 1 follows f(x 2) < f(x 1), then the function f(x) is called diminishing... A function that only increases or only decreases is called monotonous.

Limited and unlimited functions. The function is called limited if there is such a positive number M what | f(x) | M for all values x. If no such number exists, then the function - unlimited.

EXAMPLE

The function depicted in Figure 3 is limited, but not monotonic. The function in Figure 4 is just the opposite, monotonous but unlimited. (Explain this, please!).

Continuous and discontinuous functions. Function y = f (x) is called continuous at the pointx = a, if:

1) the function is defined at x = a, i.e. f (a) exists;

2) exists finite limit lim f (x) ;

x→a

(see "Function limits")

3) f (a) = lim f (x) .

x→a

If at least one of these conditions is not met, then the function is called discontinuous at the point x = a.

If the function is continuous in of all points of its domain of definition then it is called continuous function.

Even and odd functions. If for any x f(- x) = f (x), then the function is called even; if it takes place: f(- x) = - f (x), then the function is called odd... Even function graph symmetric about the Y-axis(Fig. 5), a graph of an odd function Simmetric with respect to the origin(fig. 6).

Periodic function. Function f (x) - periodic if there is such nonzero number T what for any x from the domain of the function definition takes place: f (x + T) = f (x). Such least the number is called period of function... All trigonometric functions are periodic.

EXAMPLE 1. Prove that sin x has a period of 2.

Solution. We know that sin ( x + 2n) = sin x, where n= 0, ± 1, ± 2, ...

Therefore, Appendix 2 n to the sine argument is not

Changes its meaning. Is there another number with such

Same property?

Let's pretend that P- such a number, i.e. equality:

Sin ( x + P) = sin x,

Valid for any value x... But then it has

Place and at x= / 2, i.e.

Sin (/ 2 + P) = sin / 2 = 1.

But according to the reduction formula sin (/ 2 + P) = cos P... Then

It follows from the last two equalities that cos P= 1, but we

We know that this is true only when P = 2n... Since the smallest

A nonzero number of 2 n is 2, then this number

And there is a period of sin x... It can be proved similarly that 2 from n is, therefore, this is the period sin 2 x.

Function zeros. The value of the argument at which the function is equal to 0 is called zero (root) function... A function can have multiple zeros. For example, a function y = x (x + 1) (x-3) has three zeros: x= 0, x= -1, x= 3. Geometrically function zero - this is the abscissa of the point of intersection of the function graph with the axis NS .

Figure 7 shows a graph of a function with zeros: x= a, x = b and x= c.

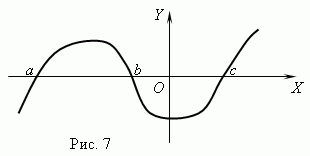
Asymptote. If the graph of a function unrestrictedly approaches some straight line at its distance from the origin, then this straight line is called asymptote.

Function zeros
The zero of a function is that value NS, at which the function becomes 0, that is, f (x) = 0.

Zeros are the points of intersection of the function graph with the axis Oh.

Parity function
A function is called even if for any NS from the domain, the equality f (-x) = f (x)

The even function is symmetric about the axis OU

Odd function
A function is called odd if for any NS from the domain, the equality f (-x) = -f (x) is fulfilled.

The odd function is symmetric about the origin.
A function that is neither even nor odd is called a function. general view.

Increasing function
A function f (x) is called increasing if more meaning the argument corresponds to the larger value of the function, i.e.

Descending function
The function f (x) is called decreasing if the larger value of the argument corresponds to the smaller value of the function, i.e.

The intervals at which the function either only decreases or only increases are called intervals of monotony... The function f (x) has 3 monotonicity intervals:

Find intervals of monotony using the Service Ascending and descending function intervals

Local maximum
Point x 0 is called a local maximum point if for any NS from the vicinity of the point x 0 the inequality holds: f (x 0)> f (x)

Local minimum
Point x 0 is called a point of local minimum if for any NS from the vicinity of the point x 0 the inequality holds: f (x 0)< f(x).

Local maximum points and local minimum points are called local extremum points.

points of local extremum.

Periodicity of function
The function f (x) is called periodic, with a period T if for any NS the equality f (x + T) = f (x) holds.

Intervals of constancy
The intervals on which the function is either only positive or only negative are called intervals of constancy.

Continuity of function
A function f (x) is called continuous at a point x 0 if the limit of the function as x → x 0 is equal to the value of the function at this point, i.e. .

Break points
The points at which the continuity condition is violated are called points of discontinuity of the function.

x 0- break point.

General scheme for plotting function graphs

1. Find the domain of definition of the function D (y).

2. Find the points of intersection of the graph of functions with the coordinate axes.

3. Examine the function for even or odd parity.

4. Examine the function for periodicity.

5. Find the intervals of monotonicity and extremum points of the function.

6. Find the convexity intervals and inflection points of the function.

7. Find the asymptotes of the function.

8. Build a graph based on the research results.

Example: Examine the function and plot its graph: y = x 3 - 3x

1) The function is defined on the entire numerical axis, i.e., its domain of definition is D (y) = (-∞; + ∞).

2) Find the points of intersection with the coordinate axes:

with the OX axis: solve the equation x 3 - 3x = 0

with axis ОY: y (0) = 0 3 - 3 * 0 = 0

3) Let's find out if the function is even or odd:

y (-x) = (-x) 3 - 3 (-x) = -x 3 + 3x = - (x 3 - 3x) = -y (x)

It follows that the function is odd.

4) The function is non-periodic.

5) Find the intervals of monotonicity and the extremum points of the function: y ’= 3x 2 - 3.

Critical points: 3x 2 - 3 = 0, x 2 = 1, x = ± 1.

y (-1) = (-1) 3 - 3 (-1) = 2

y (1) = 1 3 - 3 * 1 = -2

6) Find the convexity intervals and inflection points of the function: y ’’ = 6x

Critical points: 6x = 0, x = 0.

y (0) = 0 3 - 3 * 0 = 0

7) The function is continuous, it has no asymptotes.

8) Based on the results of the study, we will build a graph of the function.

Limits and continuity

The sets

Under the multitude a set of homogeneous objects is understood. Objects that form a set are called elements or dots this set. Sets are denoted in uppercase letters, and their elements are denoted in lowercase. If a is part of the set A, then the notation is used aÎ A... If b not a member of the set A, then it is written like this: b Ï A... A set that does not contain any elements is called an empty set and is denoted as follows: Ø.

If the set B consists of a part of the elements of the set A or coincides with it, then the set B are called subset sets and denote BÌ A.

The two sets are called equal if they consist of the same elements.

Consolidation two sets A and B called the set C, consisting of all elements belonging to at least one of the sets: C=AÈ B.

Crossing two sets A and B called the set C, consisting of all elements belonging to each of the given sets: C=AÇ B.

Difference sets A and B called the set E A that do not belong to the set B: .

Supplement multitudes AÌ B called the set C consisting of all elements of the set B not belonging A.

Sets whose elements are real numbers are called numerical:

Wherein NÌ ZÌ QÌ R, IÌ R and R=IÈ Q.

Lots of X whose elements satisfy the inequality is called segment(segment) and denoted by [ a; b]; inequality a<x<b – interval and is denoted by (); inequalities and - half-intervals and are denoted by and, respectively. You also often have to deal with infinite intervals and half-intervals:,,, and. All of them are convenient to call intervals .

Interval, i.e. the set of points satisfying the inequality (where), called the -neighborhood of the point a.

Function concept. Basic properties of the function

If each element x multitudes X matches a single element y multitudes Y, then they say that on the set X given function y=f(x). Wherein x are called independent variable or argument, a y – dependent variable or function, a f denotes the law of correspondence. Lots of X are called scope functions, and the set Y – range functions.

There are several ways to define functions.

1) Analytical method - the function is given by a formula of the form y=f(x).

2) Tabular method - the function is specified by a table containing the values ​​of the argument and the corresponding function values y=f(x).

3) Graphical way - the image of the graph of the function, i.e. the set of points ( x; y) of the coordinate plane, the abscissas of which represent the values ​​of the argument, and the ordinates are the corresponding values ​​of the function y=f(x).

4) Verbal way - the function is described by the rule of its composition. For example, the Dirichlet function takes on the value 1 if x Is a rational number and 0 if x Is an irrational number.

The following main properties of functions are distinguished.

1 Even and odd Function y=f(x) is called even if for any values x from the domain of its definition, f(–x)=f(x), and odd, if f(–x)=–f(x). If none of the listed equalities hold, then y=f(x) is called general function... The graph of an even function is symmetrical about the axis Oy, and the graph of the odd function is symmetric about the origin.

2 Monotony Function y=f(x) is called increasing (diminishing) on the interval X, if the larger value of the argument from this interval corresponds to the larger (smaller) value of the function. Let be x 1 ,x 2 Î X, x 2 >x 1 . Then the function increases on the interval X, if f(x 2)>f(x 1), and decreases if f(x 2)<f(x 1).

Along with increasing and decreasing functions, non-decreasing and non-increasing functions are considered. The function is called non-decreasing (non-increasing) if for x 1 ,x 2 Î X, x 2 >x 1 the inequality f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).

Increasing and decreasing functions, as well as non-increasing and non-decreasing functions, are called monotone.

3 Limitations Function y=f(x) is called bounded on the interval X if there is such a positive number M> 0 such that | f(x)|≤M for anyone xÎ X... V otherwise the function is called unlimited on X.

4 Frequency Function y=f(x) is called periodic with a period T≠ 0 if for any x from function domain f(x+T)=f(x). In what follows, a period will mean the smallest positive period of a function.

The function is called explicit if it is given by a formula of the form y=f(x). If the function is given by the equation F(x, y) = 0 not allowed relative to dependent variable y then they call it implicit.

Let be y=f(x) is a function of the independent variable defined on the set X with range Y... Let's put in correspondence to each yÎ Y single meaning xÎ X at which f(x)=y. Then the resulting function x=φ (y) defined on the set Y with range X is called reverse and denoted y=f –1 (x). The graphs of mutually inverse functions are symmetric with respect to the bisector of the first and third coordinate quarters.

Let the function y=f(u) is a function of the variable u defined on the set U with range Y and the variable u in turn is a function u=φ (x) defined on the set X with range U... Then given on the set X function y=f(φ (x)) is called complex function(a composition of functions, a superposition of functions, a function of a function).

Elementary functions

The main elementary functions include:

• power function y=x n; y=x - n and y=x 1/ n;
• exponential function y=a x;
• logarithmic function y= log a x;
• trigonometric functions y= sin x, y= cos x, y= tg x and y= ctg x;
• inverse trigonometric functions y= arcsin x, y= arccos x, y= arctg x and y= arcctg x.

New functions can be obtained from basic elementary functions using algebraic operations and superposition of functions.

Functions constructed from basic elementary functions using a finite number of algebraic operations and a finite number of superposition operations are called elementary.

Algebraic is called a function in which a finite number of algebraic operations are performed over the argument. Algebraic functions include:

Entire rational function (polynomial or polynomial)

Fractional rational function (ratio of two polynomials)

· An irrational function (if there is a root extraction as part of operations on an argument).

Any non-algebraic function is called transcendental... Transcendental functions include exponential, logarithmic, trigonometric, inverse trigonometric functions.

Functions and their properties

Function is one of the most important mathematical concepts.Function such a dependence of the variable y on the variable x is called such that each value of the variable x corresponds to a single value of the variable y.

Variable NS are called independent variable or argument. Variable at are called dependent variable. It is also said thatthe variable y is a function of the variable x. The dependent variable values ​​are calledfunction values.

If the dependency of a variableat from variableNS is a function, then it is briefly written as follows:y= f( x ). (Read:at equalsf fromNS .) The symbolf( x) denote the function value corresponding to the argument value equal toNS .

All values ​​of the independent variable formfunction domain . All values ​​that the dependent variable takes formfunction range .

If a function is specified by a formula and its scope is not specified, then the scope of the function is considered to consist of all the values ​​of the argument for which the formula makes sense.

Ways to set the function:

1.analytical method (the function is set using a mathematical formula;

2. table method (the function is set using the table)

3.descriptive way (function is given by verbal description)

4.graphic method (the function is set using the graph).

Function graph call the set of all points of the coordinate plane, the abscissas of which are equal to the values ​​of the argument, and the ordinates - corresponding function values.

BASIC FEATURES OF THE FUNCTIONS

1. Function zeros

Function zero is an argument value at which the function value is equal to zero..

2. Intervals of constancy of function

The intervals of constant sign of a function are such sets of argument values, on which the values ​​of the function are only positive or only negative.

3. Increasing (decreasing) function.

Increasing in a certain interval, a function is a function for which a larger value of the argument from this interval corresponds to a larger value of the function.

Function y = f ( x ) called increasing on the interval (a; b ), if for any x 1 and x 2 from this interval such thatx 1 < x 2 , the inequality is truef ( x 1 )< f ( x 2 ).

Decreasing in a certain interval, a function is a function in which a larger value of an argument from this interval corresponds to a smaller value of a function.

Function at = f ( x ) called diminishing on the interval (a; b ) if for any x 1 and x 2 from this interval such that x 1 < x 2 , the inequality is truef ( x 1 )> f ( x 2 ).

4. Parity (odd) function

Even function - a function whose domain of definition is symmetric about the origin and for anyNS from the domain, the equalityf (- x ) = f ( x ) ... The graph of an even function is symmetric about the ordinate axis.

For example, y = x 2 is an even function.

Odd function- a function whose domain of definition is symmetric about the origin and for any NS the domain of definition satisfies the equality f (- x ) = - f (x ). The graph of an odd function is symmetric about the origin.

For example: y = x 3 - odd function .

General function is not even or odd (y = x 2 + x ).

Properties of some functions and their graphics

1. Linear function is called a function of the form , where k and b - numbers.

The domain of a linear function is a setR real numbers.

Linear function graphat = kx + b ( k ≠ 0) is a straight line passing through the point (0;b ) and parallel lineat = kx .

Straight, not parallel to the axisOU, is a graph of a linear function.

Linear function properties.

1. When k > 0 function at = kx + b

2. When k < 0 function y = kx + b decreasing in the domain of definition.

y = kx + b ( k ≠ 0 ) is the whole number line, i.e. lots ofR real numbers.

At k = 0 the set of values ​​of the functiony = kx + b consists of one numberb .

3. When b = 0 and k = 0 the function is neither even nor odd.

At k = 0 the linear function has the formy = b and at b ≠ 0 it is even.

At k = 0 and b = 0 the linear function has the formy = 0 and are both odd and even.

Linear function graphy = b is the line passing through the point (0; b ) and parallel to the axisOh. Note that for b = 0 function graphy = b coincide with the axis Oh .

5. When k > 0 we have that at> 0 if and at< 0 if. At k < 0 we have that y> 0 if and at< 0, если .

2. Function y = x 2

Rreal numbers.

By attaching to a variableNS several values ​​from the domain of the function and calculating the corresponding valuesat according to the formula y = x 2 , we represent the graph of the function.

Function graph y = x 2 called parabola.

Properties of the function y = x 2 .

1. If NS= 0, then y = 0, i.e. the parabola has a common point with the coordinate axes (0; 0) - the origin.

2. If x ≠ 0 , then at > 0, i.e. all points of the parabola, except for the origin, lie above the abscissa axis.

3. The set of values ​​of the functionat = NS 2 is the span functionat = NS 2 decreases.

NS

3.Function

The scope of this function is the span functiony = | x | decreases.

7. The function takes the smallest value at the pointNS, it is equal to 0. Highest value does not exist.

6. Function

Function scope: .

Function range: .

The graph is a hyperbole.

1. Zeros of the function.

at ≠ 0, no zeros.

2. Intervals of constancy,

If k > 0, then at> 0 for NS > 0; at < 0 при NS < О.

If k < 0, то at < 0 при NS > 0; at> 0 for NS < 0.

3. Intervals of increasing and decreasing.

If k > 0, then the function decreases as .

If k < 0, то функция возрастает при .

4. Parity (oddness) of the function.

The function is odd.

Square trinomial

Equation of the form ax 2 + bx + c = 0, where a , b and with - some numbers, moreovera ≠ 0 is called square.

In a quadratic equationax 2 + bx + c = 0 coefficient a called the first coefficient, b - second coefficients, s - free member.

Root formula quadratic equation looks like:

.

The expression is called discriminant quadratic equation and is denoted byD .

If D = 0, then there is only one number satisfying the equation ax 2 + bx + c = 0. However, we agreed to say that in this case the quadratic equation has two equal real roots, and the number itself are called double root.

If D < 0, то квадратное уравнение не имеет действительных корней.

If D > 0, then the quadratic equation has two different real roots.

Let a quadratic equation be givenax 2 + bx + c = 0. Since a ≠ 0, then, dividing both sides of this equation bya, we get the equation ... Assuming and , we arrive at the equation , in which the first coefficient is equal to 1. Such an equation is calledgiven.

The formula for the roots of the reduced quadratic equation is:

.

Equations of the form

a x 2 + bx = 0, ax 2 + with = 0, a x 2 = 0

are called incomplete quadratic equations. Incomplete quadratic equations are solved by factoring the left side of the equation.

Vieta's theorem .

The sum of the roots of the quadratic equation is equal to the ratio of the second coefficient to the first, taken with the opposite sign, and the product of the roots is the ratio of the free term to the first coefficient, i.e.

Converse theorem.

If the sum of any two numbersNS 1 and NS 2 is equal to , and their product is, then these numbers are the roots of the quadratic equationOh 2 + b x + c = 0.

View function Oh 2 + b x + c called square trinomial. The roots of this function are the roots of the corresponding quadratic equationOh 2 + b x + c = 0.

If the discriminant square trinomial is greater than zero, then this trinomial can be represented as:

Oh 2 + b x + c = a (x-x 1 ) (x-x 2 )

where NS 1 and NS 2 - roots of a trinomial

If the discriminant of a square trinomial is zero, then this trinomial can be represented as:

Oh 2 + b x + c = a (x-x 1 ) 2

where NS 1 is a root of a trinomial.

For example, 3x 2 - 12x + 12 = 3 (x - 2) 2 .

Equation of the form Oh 4 + b NS 2 + with= 0 is called biquadratic. By replacing a variable using the formulaNS 2 = y it is reduced to a quadratic equationa y 2 + by + c = 0.

Quadratic function

Quadratic function is called a function that can be written by a formula of the formy = ax 2 + bx + c , where x - independent variable,a , b and c - some numbers, moreovera ≠ 0.

The properties of the function and the type of its graph are determined mainly by the values ​​of the coefficienta and discriminant.

Properties of a quadratic function

Domain:R;

Range of values:

at a > 0 [- D/(4 a); ∞)

at a < 0 (-∞; - D/(4 a)];

Even, odd:

at b = 0 the function is even

at b ≠ 0 function is neither even nor odd

at D> 0 two zeros:,

at D= 0 one zero:

at D < 0 нулей нет

Intervals of constancy:

if, a> 0, D> 0, then

if, a> 0, D= 0, then

e if a> 0, D < 0, то

if a< 0, D> 0, then

if a< 0, D= 0, then

if a< 0, D < 0, то

- Intervals of monotony

for a> 0

at a< 0

The graph of a quadratic function isparabola - curve symmetrical about a straight line passing through the vertex of the parabola (the vertex of the parabola is the point of intersection of the parabola with the axis of symmetry).

To plot a quadratic function graph, you need:

1) find the coordinates of the vertex of the parabola and mark it in the coordinate plane;

2) build a few more points belonging to the parabola;

3) connect the marked points with a smooth line.

The coordinates of the vertex of the parabola are determined by the formulas:

; .

Convert function graphs

1. Stretching graphicsy = x 2 along the axisat v| a | times (at| a | < 1 is a compression to 1 /| a | once).

If, and< 0, произвести, кроме того, зеркальное отражение графика отно­сительно оси NS (the branches of the parabola will be directed downward).

Result: function graphy = ah 2 .

2. Parallel transfer function graphicsy = ah 2 along the axisNS on| m | (to the right at

m > 0 and to the left forT< 0).

Result: function graphy = a (x - t) 2 .

3. Parallel transfer function graphics along the axisat on| n | (up atn> 0 and down atNS< 0).

Result: function graphy = a (x - t) 2 + p.

Quadratic inequalities

Inequalities of the formOh 2 + b x + c> 0 andOh 2 + bx + c< 0, whereNS - variable,a , b andwith - some numbers, moreover,a ≠ 0 are called inequalities of the second degree with one variable.

Solving a second-degree inequality in one variable can be viewed as finding the intervals in which the corresponding quadratic function takes positive or negative values.

To solve inequalities of the formOh 2 + bx + c> 0 andOh 2 + bx + c< 0 do the following:

1) find the discriminant of a square trinomial and find out whether the trinomial has roots;

2) if the trinomial has roots, then mark them on the axisNS and through the marked points, a parabola is drawn schematically, the branches of which are directed upward ata > 0 or down ata< 0; if the trinomial has no roots, then schematically depict a parabola located in the upper half-plane ata > 0 or at the bottom ata < 0;

3) find on the axisNS intervals for which the parabola points are located above the axisNS (if the inequality is solvedOh 2 + bx + c> 0) or below the axisNS (if the inequality is solvedOh 2 + bx + c < 0).

Example:

Solve the inequality .

Consider the function

Its graph is a parabola, the branches of which are directed downward (because. ).

Let's find out how the graph is located relative to the axisNS. For this we solve the equation ... We get thatx = 4. The equation has a single root. Hence, the parabola touches the axisNS.

Sketching a parabola, we find that the function takes negative values ​​for anyNS, except 4.

The answer can be written like this:NS - any number not equal to 4.

Solving inequalities using the interval method

solution scheme

1. Find zeros the function on the left side of the inequality.

2. Mark the position of the zeros on the numerical axis and determine their multiplicity (ifk i is even, then zero of even multiplicity, ifk i odd - then odd).

3. Find the signs of a function in the intervals between its zeros, starting from the rightmost interval: in this interval, the function on the left side of the inequality is always positive for the reduced form of inequalities. When passing from right to left through the zero of a function from one gap to an adjacent one, one should take into account:

if zero is odd multiplicity, the sign of the function changes,

if zero is even multiplicity, the sign of the function is preserved.

4. Record your answer.

Example:

(x + 6) (x + 1) (NS - 4) < 0.

Found function zeros. They are equal:NS 1 = -6; NS 2 = -1; NS 3 = 4.

We mark on the coordinate line the zeros of the functionf ( x ) = (x + 6) (x + 1) (NS - 4).

Let us find the signs of this function in each of the intervals (-∞; -6), (-6; -1), (-1; 4) and

The figure shows that the set of solutions to the inequality is the union of the intervals (-∞; -6) and (-1; 4).

Answer: (-∞ ; -6) and (-1; 4).

The considered method for solving inequalities is calledby the method of intervals.

The methodological material is for reference and covers a wide range of topics. The article provides an overview of the graphs of the main elementary functions and considers the most important issue - how to build a graph correctly and QUICKLY... In the course of studying higher mathematics without knowing the graphs of the main elementary functions, it will be difficult, therefore it is very important to remember how the graphs of a parabola, hyperbola, sine, cosine, etc. look like, to remember some values ​​of the functions. We will also talk about some of the properties of the main functions.

I do not claim the completeness and scientific thoroughness of the materials, the emphasis will be made, first of all, in practice - those things with which one has to deal with literally at every step, in any topic of higher mathematics... Charts for dummies? You can say so.

By popular demand from readers clickable table of contents:

In addition, there is an ultra-short synopsis on the topic
- master 16 types of charts by studying SIX pages!

Seriously, six, even I was surprised. This synopsis contains improved graphics and is available for a token fee, a demo version can be viewed. It is convenient to print the file so that the graphs are always at hand. Thanks for supporting the project!

And immediately we begin:

How to plot the coordinate axes correctly?

In practice, tests are almost always drawn up by students in separate notebooks, lined in a cage. Why do you need checkered lines? After all, the work, in principle, can be done on A4 sheets. And the cage is necessary just for high-quality and accurate design of drawings.

Any drawing of a graph of a function starts with coordinate axes.

Drawings are available in 2D and 3D.

Consider first the two-dimensional case cartesian rectangular coordinate system:

1) We draw the coordinate axes. The axis is called abscissa and the axis is y-axis ... We always try to draw them neat and not crooked... The arrows should also not resemble Papa Carlo's beard.

2) We sign the axes with capital letters "X" and "Y". Do not forget to sign the axes.

3) Set the scale along the axes: draw zero and two ones... When performing a drawing, the most convenient and common scale is: 1 unit = 2 cells (drawing on the left) - if possible, stick to it. However, from time to time it happens that the drawing does not fit on the notebook sheet - then we reduce the scale: 1 unit = 1 cell (drawing on the right). Rarely, but it happens that the scale of the drawing has to be reduced (or increased) even more

DO NOT NEED to "scribble with a machine gun" ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... For coordinate plane- not a monument to Descartes, and a student - not a dove. We put zero and two units along the axes... Sometimes instead of units, it is convenient to "mark" other values, for example, "two" on the abscissa and "three" on the ordinate - and this system (0, 2 and 3) will also unambiguously set the coordinate grid.

It is better to estimate the estimated dimensions of the drawing BEFORE the drawing is built.... So, for example, if the task requires you to draw a triangle with vertices,,, then it is quite clear that the popular scale of 1 unit = 2 cells will not work. Why? Let's look at the point - here you have to measure fifteen centimeters down, and, obviously, the drawing will not fit (or barely fit) on a notebook sheet. Therefore, we immediately select a smaller scale of 1 unit = 1 cell.

By the way, about centimeters and notebook cells. Is it true that 30 tetrad cells contain 15 centimeters? Measure in a notebook for interest 15 centimeters with a ruler. In the USSR, perhaps this was true ... It is interesting to note that if you measure these very centimeters horizontally and vertically, the results (in cells) will be different! Strictly speaking, modern notebooks are not checkered, but rectangular. Perhaps this will seem nonsense, but drawing, for example, a circle with a compass in such layouts is very inconvenient. To be honest, at such moments you start to think about the correctness of Comrade Stalin, who was sent to camps for hack work in production, not to mention the domestic automotive industry, falling planes or exploding power plants.

Speaking of quality, or a brief recommendation for stationery. Today, most of the notebooks are on sale, not to say bad words, full of homosexuality. For the reason that they get wet, and not only from gel pens, but also from ballpoint pens! They save on paper. For registration control works I recommend using the notebooks of the Arkhangelsk PPM (18 sheets, cage) or "Pyaterochka", although it is more expensive. It is advisable to choose a gel pen, even the cheapest Chinese gel refill is much better than a ballpoint pen that either smears or tears the paper. The only "competitive" ballpoint pen in my memory is "Erich Krause". She writes clearly, beautifully and stably - either with a full core or with an almost empty one.

Additionally: Seeing a rectangular coordinate system through the eyes of analytical geometry is covered in the article Linear (non) dependence of vectors. Basis of vectors, detailed information on coordinate quarters can be found in the second paragraph of the lesson Linear inequalities.

Three-dimensional case

It's almost the same here.

1) We draw the coordinate axes. Standard: axis applicate - directed upwards, axis - directed to the right, axis - left and down strictly at an angle of 45 degrees.

2) We sign the axes.

3) Set the scale along the axes. Axis scale - half the scale on other axes... Also notice that in the drawing on the right I have used a non-standard "serif" along the axis (this possibility has already been mentioned above)... From my point of view, this is more accurate, faster and more aesthetically pleasing - there is no need to look for the middle of a cell under a microscope and "sculpt" a unit right next to the origin.

When doing 3D drawing again - give priority to scale
1 unit = 2 cells (drawing on the left).

What are all these rules for? Rules are there to be broken. What I'm going to do now. The fact is that the subsequent drawings of the article will be made by me in Excel, and the coordinate axes will look incorrect from the point of view of correct design. I could draw all the charts by hand, but drawing them is actually terrible as Excel will draw them much more accurately.

Graphs and basic properties of elementary functions

The linear function is given by the equation. The graph of linear functions is straight... In order to build a straight line, it is enough to know two points.

Example 1

Plot the function. Let's find two points. It is advantageous to choose zero as one of the points.

If, then

Take some other point, for example, 1.

If, then

When filling out tasks, the coordinates of the points are usually summarized in a table:

And the values ​​themselves are calculated orally or on a draft, calculator.

Two points are found, let's execute the drawing:

When drawing up a drawing, we always sign graphs.

It will not be superfluous to recall special cases of a linear function:

Notice how I have arranged the signatures, signatures should not allow discrepancies when studying the drawing... In this case, it was highly undesirable to put a signature near the point of intersection of lines, or at the bottom right between the graphs.

1) A linear function of the form () is called direct proportionality. For example, . The direct proportional graph always passes through the origin. Thus, the construction of a straight line is simplified - it is enough to find only one point.

2) The equation of the form sets a straight line parallel to the axis, in particular, the axis itself is set by the equation. The function graph is built immediately, without finding any points. That is, the record should be understood as follows: "the game is always equal to –4, for any value of x".

3) The equation of the form sets a straight line parallel to the axis, in particular, the axis itself is set by the equation. The function graph is also built immediately. The notation should be understood as follows: "x is always, for any value of y, is equal to 1".

Some will ask, why remember the 6th grade ?! This is how it is, maybe so, only over the years of practice, I met a dozen students who were perplexed by the task of building a graph like or.

Drawing a straight line is the most common step in drawing.

The straight line is considered in detail in the course of analytical geometry, and those who wish can refer to the article Equation of a straight line on a plane.

Quadratic, cubic function graph, polynomial graph

Parabola. Quadratic Function Plot () is a parabola. Consider the famous case:

Let's recall some of the properties of the function.

So, the solution to our equation: - it is at this point that the vertex of the parabola is located. Why this is so, you can find out from the theoretical article on the derivative and the lesson on the extrema of a function. In the meantime, we calculate the corresponding value of the "game":

So the vertex is at the point

Now we find other points, while brazenly using the symmetry of the parabola. It should be noted that the function – is not even, but, nevertheless, the symmetry of the parabola has not been canceled.

In what order to find the rest of the points, I think, it will be clear from the final table:

This construction algorithm can be figuratively called a "shuttle" or the "back and forth" principle with Anfisa Chekhova.

Let's execute the drawing:

One more useful sign comes to mind from the graphs examined:

For a quadratic function () the following is true:

If, then the branches of the parabola are directed upwards.

If, then the branches of the parabola are directed downward.

In-depth knowledge of the curve can be obtained in the Hyperbola and Parabola lesson.

A cubic parabola is given by a function. Here is a drawing familiar from school:

Let's list the main properties of the function

Function graph

It represents one of the branches of the parabola. Let's execute the drawing:

The main properties of the function:

In this case, the axis is vertical asymptote for the graph of the hyperbola at.

It will be a GREAT mistake if you neglect to allow the intersection of the graph with the asymptote when drawing up the drawing.

Also one-sided limits tell us that the hyperbola not limited from above and not limited from below.

Let us examine the function at infinity: that is, if we begin to move along the axis to the left (or to the right) to infinity, then the "games" will be infinitely close approach zero, and, accordingly, the branches of the hyperbola infinitely close approach the axis.

So the axis is horizontal asymptote for the graph of the function, if "x" tends to plus or minus infinity.

The function is odd, and, hence, the hyperbola is symmetric about the origin. This fact is obvious from the drawing, in addition, it is easily verified analytically: .

The graph of a function of the form () represents two branches of the hyperbola.

If, then the hyperbola is located in the first and third coordinate quarters(see picture above).

If, then the hyperbola is located in the second and fourth coordinate quarters.

The indicated regularity of the place of residence of the hyperbola is easy to analyze from the point of view of geometric transformations of the graphs.

Example 3

Construct the right branch of the hyperbola

We use the point-by-point construction method, while it is advantageous to select the values ​​so that it is divided entirely:

Let's execute the drawing:

It will not be difficult to construct the left branch of the hyperbola, here the odd function will just help. Roughly speaking, in the table of point-by-point construction, mentally add a minus to each number, put the corresponding points and draw a second branch.

Detailed geometric information about the considered line can be found in the article Hyperbola and Parabola.

Exponential function graph

In this section, I will immediately consider the exponential function, since in problems of higher mathematics in 95% of cases it is the exponential that is encountered.

Let me remind you that - this is an irrational number: this will be required when building a schedule, which, in fact, I will build without ceremony. Three points perhaps enough:

Let's leave the function graph alone for now, more on that later.

The main properties of the function:

In principle, function graphs look the same, etc.

I must say that the second case is less common in practice, but it does occur, so I considered it necessary to include it in this article.

Logarithmic function graph

Consider a function with natural logarithm.
Let's execute a point-by-point drawing:

If you have forgotten what a logarithm is, please refer to your school textbooks.

The main properties of the function:

Domain:

Range of values:.

The function is not limited from above: , albeit slowly, but the branch of the logarithm goes up to infinity.
Let us examine the behavior of the function near zero on the right: ... So the axis is vertical asymptote for the graph of the function with "x" tending to zero on the right.

It is imperative to know and remember the typical value of the logarithm.: .

In principle, the graph of the base logarithm looks the same:,, (decimal logarithm base 10), etc. Moreover, the larger the base, the flatter the graph will be.

We will not consider the case, for some reason I don’t remember the last time I built a graph with such a basis. And the logarithm seems to be a very rare guest in problems of higher mathematics.

At the end of the paragraph, I will say about one more fact: Exponential function and logarithmic functionAre two mutually inverse functions... If you look closely at the graph of the logarithm, you can see that this is the same exponent, it is just that it is located a little differently.

Trigonometric function graphs

How does trigonometric torment begin at school? Right. From the sine

Let's plot the function

This line is called sinusoid.

Let me remind you that "pi" is an irrational number:, and in trigonometry it dazzles in the eyes.

The main properties of the function:

This function is periodic with a period. What does it mean? Let's look at the segment. To the left and to the right of it, exactly the same piece of the graph is repeated endlessly.

Domain:, that is, for any value of "x" there is a sine value.

Range of values:. The function is limited:, that is, all the "gamers" sit strictly in the segment.
This does not happen: or, more precisely, it happens, but these equations have no solution.