In this lesson, we will look at each of these operations separately.

Design of lesson

Addition of decimal fractions

As we know, the decimal fraction has a whole and fractional part. When adding decimal fractions, integers and fractional parts are detached separately.

For example, lay decimal fractions 3.2 and 5.3. Decimals more conveniently folded in a column.

We prepare first these two fractions in the column, while the whole parts must be under whole, and fractional under fractional. At school this requirement is called "Comma dressed".

We write the fraction in the column so that the comma is filled:

We begin to add fractional parts: 2 + 3 \u003d 5. We write on the top five in the fractional part of our answer:

Now we fold entire parts: 3 + 5 \u003d 8. Record the eight in the whole part of our answer:

Now separate the semicolons the whole part of the fractional. To do this, again, we observe the rule "Comma dressed":

Received an answer 8.5. It means expressions 3,2 + 5,3 equals 8.5

In fact, not everything is so simple, as it seems at first glance. Here, too, there are their underwater stones, which we will talk about.

Discharges in decimal fractions

In decimal fractions, as in ordinary numbers, there are their discharges. These are discharges of the tenths, the discharge of hundredths, the discharges of thousands. At the same time, the discharge begins after the comma.

The first digit after the comma is responsible for the discharge of the tenths, the second digit after the comma for the discharge of hundredths, the third digit after the comma for the discharge of thousands.

Discharges in decimal fractions keep some useful information. In particular, they report how much in decimal fractions of the tenths, hundredths and thousands of units.

For example, consider the decimal fraction 0,345

The position where the triple is called discharge of tenths

The position where the four is called discharge of hundredths

Position where the fide is called the discharge of thousands

Let's look at this picture. We see that in the discharge of the tenths there is a triple. This suggests that in the decimal fraction 0.345 contains three tenths.

If we fold the fractions, and then we get the original decimal fraction 0,345

It can be seen that at first we got the answer, but transferred it to the decimal fraction and got 0.345.

In addition, decimal fractions are complied with the same principles and rules as when the usual numbers are addition. The addition of decimal fractions occurs in discharges: the tenths are folded with tenth parts, hundredths with hundredths, thousandths with thousands.

Therefore, when adding decimal fractions, you need to comply with the rule "Comma dressed". The comma dive ensures that the very order in which the tenths add up with tits, hundredths with hundredths, thousands of thousands.

Example 1. Find the value of expression 1.5 + 3.4

First of all, we fold fractional parts 5 + 4 \u003d 9. We write down the nine in the fractional part of our answer:

Now we fold entire parts 1 + 3 \u003d 4. Record the fourth in the whole part of our answer:

Now separate the semicolons the whole part of the fractional. To do this, again, we comply with the "comma dive" rule:

Received an answer 4.9. So the value of the expression is 1.5 + 3.4 is 4.9

Example 2. Find an expression value: 3.51 + 1.22

Write down in the column this expression, compliance with the rule "comma dirt"

First of all, we fold the fractional part, namely the hundredths of the 1 + 2 \u003d 3. We write down the top three in the hundredth of our answer:

Now we fold the tenths of 5 + 2 \u003d 7. We write a seven in the tenth of our answer:

Now we fold entire parts 3 + 1 \u003d 4. We write down the fourth in the whole part of our answer:

Separate the semicolons, the whole part of the fractional, observing the "comma-filled" rule:

Received the answer 4.73. So the value of expression 3.51 + 1,22 is 4.73

3,51 + 1,22 = 4,73

As in conventional numbers, with the addition of decimal fractions can occur. In this case, one digit is written in response, and the rest are transferred to the next discharge.

Example 3. Find an expression value 2.65 + 3,27

We write in the column This expression:

We fold the cells 5 + 7 \u003d 12. The number 12 does not fit in a hundredth of our response. Therefore, in the cell of the part, we write the number 2, and the unit is transferred to the next discharge:

Now we fold the tenths of 6 + 2 \u003d 8 plus a unit that got from the previous operation, we get 9. Record number 9 in the tenth of our answer:

Now we fold entire parts 2 + 3 \u003d 5. Record 5 in the whole part of our answer:

Received 5.92. So the value of the expression 2.65 + 3,27 is 5.92

2,65 + 3,27 = 5,92

Example 4. Find an expression value 9.5 + 2.8

We write in the column this expression

We fold fractional parts 5 + 8 \u003d 13. The number 13 does not fit in the fractional part of our answer, so first write the number 3, and the unit is transferred to the next discharge, more precisely carry it to the integer part:

Now we fold entire parts 9 + 2 \u003d 11 plus a unit that got from the previous operation, we get 12. Record number 12 in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received 12.3. Means the value of expression 9.5 + 2.8 is 12.3

9,5 + 2,8 = 12,3

When decaying decimal fractions, the number of digits after the comma in both fractions should be the same. If the numbers are missing, then these places in the fractional part are filled with zeros.

Example 5.. Find an expression value: 12,725 + 1.7

Before recording this expression in the column, we will make the number of numbers after the comma in both fractions the same. In the decimal fraction 12.725 after the semicolons, three digits, and in the fraction 1.7 only one. So in the fraction 1.7 at the end you need to add two zero. Then we get a fraction of 1,700. Now you can write this expression in the column and start computing:

We fold the thousands of parts 5 + 0 \u003d 5. Write the figure 5 in the thousandth part of our answer:

We fold the cellular parts 2 + 0 \u003d 2. Write on the number 2 in the hundredth of our answer:

We fold the tenths 7 + 7 \u003d 14. The number 14 does not fit in the tenth of our response. Therefore, first write the number 4, and the unit is transferred to the next discharge:

Now we fold entire parts 12 + 1 \u003d 13 plus a unit that got from the previous operation, we obtain 14. Record number 14 in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received the answer 14,425. So the value of expression 12,725 + 1,700 is 14,425

12,725+ 1,700 = 14,425

Subtraction decimal fractions

When subtracting decimal fractions, it is necessary to comply with the same rules as when adding: "comma dilated" and "equal number of numbers after a comma."

Example 1. Find the value of the expression 2.5 - 2.2

We record this expression in the column, following the comma duty rule:

Calculate the fractional part 5-2 \u003d 3. Write on the figure 3 in the tenth of our answer:

Calculate the whole part 2-2 \u003d 0. Record zero in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received 0.3. So the value of expression 2.5 - 2.2 is 0.3

2,5 − 2,2 = 0,3

Example 2. Find an expression value 7,353 - 3.1

In this expression, a different number of numbers after the comma. In the fraction 7.353 after the semicolons, three digits, and in the fraction 3.1 only one. So in the fraction 3.1 at the end you need to add two zero to make the number of numbers in both fractions the same. Then we get 3,100.

Now you can write this expression in the column and calculate it:

Received 4.253 response. Means the value of expression 7,353 - 3.1 is 4.253

7,353 — 3,1 = 4,253

As in conventional numbers, sometimes they will have to occupy a unit from a neighboring discharge, if the subtraction becomes impossible.

Example 3. Find an expression value 3.46 - 2.39

We subtract the hundredth parts 6-9. From the number 6 not to subtract the number 9. Therefore, you need to take a unit from a neighboring discharge. Having taught the unit in the neighboring discharge number 6 refers to the number 16. Now you can calculate the cells of the cells 16-9 \u003d 7. We write down a seven in a hundredth of our answer:

Now we will deduct the tenths. Since we took in the discharge of the tenths of one unit, then the figure that was located there decreased by one unit. In other words, in the discharge of the tenths no longer digit 4, and the figure 3. I calculate the tenths 3-3 \u003d 0. Write zero in the tenth of our answer:

Now we will deduct the whole parts 3-2 \u003d 1. We write down the unit in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received the answer 1.07. So the value of expression 3,46-2.39 is 1.07

3,46−2,39=1,07

Example 4.. Find an expression value 3-1.2

In this example, a decimal fraction is deducted from an integer. We write this expression by the column so that whole part Decimal fraction 1,23 turned out to be at number 3

Now we will make the number of numbers after the comma are the same. For this, after the number 3, we will put a comma and add one zero:

Now we will deduct the tenths: 0-2. From zero not subtract number 2. Therefore, you need to take a unit from a neighboring discharge. Taking a unit in a neighboring discharge, 0 refers to the number 10. Now you can calculate the tenths 10-2 \u003d 8. Write the eight in the tenth of our answer:

Now deduct the whole parts. Previously, the number 3 was located in the whole, but we took it one unit. As a result, it appealed to the number 2. Therefore, from 2, we subtract 1. 2-1 \u003d 1. We write down the unit in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received an answer 1.8. Means the value of expression 3-1,2 is 1.8

Multiplying decimal fractions

Multiplying decimal fractions is simple and even fascinating. In order to multiply decimal fractions, you need to multiply them as conventional numbers, not paying attention to the commas.

Having received the answer, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in both fractions, then in response to count the right of the same number and put a comma.

Example 1. Find the value of the expression 2.5 × 1.5

Move these decimal fractions as ordinary numbers, not paying attention to the commas. In order not to pay attention to commas, it is possible to present that they are generally absent:

We received 375. In this regard, it is necessary to separate the semicolons from the fractional. To do this, it is necessary to calculate the number of digits after the comma in fractions 2.5 and 1.5. In the first fraction after the semicolons, one digit, in the second fraction, too alone. Total two digits.

Returning to the number 375 and begin to move right to left. We need to count two digits to the right and put a comma:

Received the answer 3.75. Means the value of the expression 2.5 × 1.5 is 3.75

2.5 × 1 5 \u003d 3.75

Example 2. Find an expression value 12.85 × 2.7

Alternate these decimal fractions, not paying attention to the commas:

We received 34695. In this regard, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of digits after the comma in the fractions of 12.85 and 2.7. In the fraction 12.85 after the semicolons, two digits, in the fraction 2.7 one digit - total three digits.

Returning to the number 34695 and begin to move right to left. We need to count three digits to the right and put a comma:

Received the answer 34.695. Means the value of expression 12.85 × 2.7 is 34,695

12.85 × 2,7 \u003d 34,695

Multiplication of decimal fraction on the usual number

Sometimes there are situations when you need to multiply the decimal fraction to the usual number.

In order to multiply the decimal fraction and the usual number, you need to multiply them, not paying attention to the comma in the decimal fraction. Having received the answer, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the decimal fraction, then in response to refer to the right of the same number and put the comma.

For example, multiply 2.54 to 2

We multiply the decimal fraction 2.54 to the usual number 2, not paying attention to the comma:

They received the number 508. In this regard, it is necessary to separate the semicolons the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the fraction 2.54. In the fraction 2.54 after the semicolons two digits.

Returning to the number 508 and begin to move right to left. We need to count two digits to the right and put a comma:

Received 5.08. Means the value of the expression 2.54 × 2 is 5.08

2.54 × 2 \u003d 5.08

Multiplying decimal fractions by 10, 100, 1000

The multiplication of decimal fractions by 10, 100 or 1000 is performed in the same way as the multiplication of decimal fractions into conventional numbers. You need to perform multiplication, not paying attention to the comma in the decimal fraction, then in response to separate the whole part of the fractional, squeezing the right of the same number as the numbers were after the semicolons in the decimal fraction.

For example, multiply 2.88 to 10

Multiply decimal fraction 2.88 by 10, not paying attention to the comma in decimal fraction:

Received 2880. In this regard, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the semicolon in the fraction 2.88. We see that in the fraction 2.88 after the semicolons two digits.

Returning to the number 2880 and begin to move right to left. We need to count two digits to the right and put a comma:

Received the answer 28.80. We will throw the last zero - we get 28.8. Means the value of the expression 2.88 × 10 is 28.8

2.88 × 10 \u003d 28.8

There is a second way of multiplying decimal fractions by 10, 100, 1000. This method is much easier and more convenient. It lies in the fact that the comma in the decimal fraction moves to the right to so many numbers as zeros in the multiplier.

For example, we solve the previous example of 2.88 × 10 in this way. Do not lead to any calculations, we immediately look at the multiplier 10. We are interested in how much zeros in it. We see that in it one zero. Now in the fraction 2,88 move the comma to the right to one digit, we get 28.8.

2.88 × 10 \u003d 28.8

Let's try to multiply 2.88 per 100. We immediately look at the multiplier 100. We are interested in how much zeros in it. We see that in it two zero. Now in the twist 2,88 move the comma to the right into two digits, we get 288

2.88 × 100 \u003d 288

Let's try to multiply 2.88 per 1000. We immediately look at the factor of 1000. We are interested in how much zeros in it. We see that in it three zero. Now in the twist 2,88 move the comma to the right to three digits. There are no third digits there, so we finish another zero. As a result, we get 2880.

2.88 × 1000 \u003d 2880

Multiplying decimal fractions by 0.1 0.01 and 0.001

The multiplication of decimal fractions by 0.1, 0.01 and 0.001 occurs in the same way as the multiplication of the decimal fraction for a decimal fraction. It is necessary to multiply the fractions as conventional numbers, and in response to put a comma, counting so much the numbers on the right, how many digits after a comma in both fractions.

For example, multiply 3.25 to 0.1

We multiply these fractions, as ordinary numbers, not paying attention to the commas:

Received 325. In this regard, it is necessary to separate the semicolons from the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the frauds 3.25 and 0.1. In the fraction 3.25 after the semicolons, two digits, in the fraction 0.1 one digit. Total three numbers.

We return to the number 325 and begin to move right to left. We need to count three digits to the right and put a comma. After counting the three digits, we discover that the numbers are over. In this case, you need to add one zero and put a comma:

Received 0.325. So the value of expression is 3.25 × 0.1 is 0.325

3.25 × 0.1 \u003d 0.325

There is a second method of multiplication of decimal fractions by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It lies in the fact that the comma in decimal fraction moves to the left of so many numbers as zeros in the multiplier.

For example, we solve the previous example of 3.25 × 0.1 in this way. Do not lead to any calculations immediately look at the multiplier of 0.1. We are interested in how much zeros in it. We see that in it one zero. Now in the fraction 3,25 move the comma left to one digit. After moving the comma on one digit to the left, we see that there are no more numbers before the triple. In this case, add one zero and put the comma. As a result, we get 0.325

3.25 × 0.1 \u003d 0.325

Let's try to multiply 3.25 by 0.01. We immediately look at the multiplier of 0.01. We are interested in how much zeros in it. We see that in it two zero. Now in the fraction 3,25 move the comma to the left into two digits, we get 0.0325

3.25 × 0,01 \u003d 0,0325

Let's try to multiply 3.25 by 0.001. We immediately look at the multiplier of 0.001. We are interested in how much zeros in it. We see that in it three zero. Now in the fraction 3,25 move the comma to the left of three digits, we get 0.00325

3.25 × 0.001 \u003d 0.00325

It is impossible to confuse the multiplication of decimal fractions by 0.1, 0.001 and 0.001 with multiplication by 10, 100, 1000. Typical error Most people.

When multiplying 10, 100, 1000, the comma is transferred to the right to the same number how many zeros in the multiplier.

And with multiplication by 0.1, 0.01 and 0.001, the comma is transferred to the left for the same number how many zeros in the multiplier.

If at first it is difficult to remember, you can use the first method in which multiplication is performed as with conventional numbers. In response, it will be necessary to separate the whole part of the fractional, counting the right of the same number as numbers after the comma in both fractions.

Dividing a smaller number to more. Advanced level.

In one of the previous lessons, we said that when dividing a smaller number, the fraction was greater, in the numerator of which is divisible, and in the denominator - a divider.

For example, to divide one apple for two, you need to write 1 in the numerator (one apple), and write 2 in the denominator (two friends). As a result, we will get a fraction. So each friend will get on the apple. In other words, half of the apple. Fraction is the answer to the task "How to divide one apple for two"

It turns out that it is possible to solve this problem and further if divided 1 at 2. After all, a fractional feature in any fraction means division, which means that this division is allowed. But how? We are accustomed to the fact that Delimi is always more divisor. And here on the contrary, divisible less divider.

Everything will become clear if you remember that the fraction means crushing, division, separation. And therefore, the unit can be fragmented as many parts, and not only into two parts.

When dividing a smaller number, a decimal fraction is greater, in which the whole part will be 0 (zero). The fractional part can be any.

So, we divide 1 to 2. I will solve this example:

The unit is simply not divided into two units. If you ask a question "How many twists in unity" , then the answer will be 0. Therefore, in private, write 0 and put the comma:

Now, as usual, we multiply the private on the divider to pull out the residue:

The moment came when the unit can be crushed into two parts. To do this, to the right of the received units add another zero:

Received 10. We divide 10 to 2, we get 5. Write on the top five in the fractional part of our answer:

Now pull out the last residue to complete the calculation. Multiply 5 to 2, we get 10

Received 0.5. So the fraction is equal to 0.5

Half of the apple can be recorded and with a decimal fraction 0.5. If you fold these two halves (0.5 and 0.5), we again get the original one-piece apple:

This moment can also be understood if you represent how 1 cm is divided into two parts. If 1 centimeter is divided into 2 parts, then it turns out 0.5 cm

Example 2. Find an expression value 4: 5

How many tops in the fourth? Not at all. We write in private 0 and put the comma:

We multiply 0 to 5, we get 0. Record zero under the fourth. Immediately deduct this zero from the divide:

Now let's start crushing (divide) the fourth on 5 parts. To do this, to the right of 4 add zero and divide 40 to 5, we get 8. Write the eight in private.

Complete an example, multiplying 8 to 5, and receiving 40:

Received 0.8. So the value of expression 4: 5 is 0.8

Example 3. Find an expression value 5: 125

How many numbers 125 in the five? Not at all. We write 0 in private and put a comma:

We multiply 0 to 5, we get 0. Write 0 under the top five. Immediately subtract 0 from the top five

Now let's start crushing (divide) the top five5 parts. To do this, to the right of this five watering zero:

Delim 50 to 125. How many numbers 125 are among 50? Not at all. So in private again write 0

Multiply 0 to 125, we get 0. We write this zero under 50. Immediately deduct 0 out of 50

Now we divide the number 50 to 125 parts. To do this, to the right of 50, we write another zero:

We divide 500 to 125. How many numbers 125 are among 500. Among the 500 four numbers 125. Write the fourth in private:

Complete an example, multiplying 4 to 125, and receiving 500

Received 0.04. So the value of expression 5: 125 is 0.04

Division of numbers without residue

So, we put a comma in private after the unit, thereby pointing out that the division of integral parts is over and we proceed to the fractional part:

I add zero to the residue 4

Now we divide 40 to 5, we get 8. Record eight in private:

40-40 \u003d 0. Received 0 in the remainder. So division is fully completed. When dividing 9 on 5, a decimal fraction is obtained 1.8:

9: 5 = 1,8

Example 2.. Split 84 by 5 without a residue

At first we divide 84 to 5 as usual with the residue:

Received in private 16 and another 4 in the remainder. Now we divide this residue by 5. We put in a private comma, and I add 4 to the residue 4

Now we divide 40 to 5, we get 8. We write to the eight in the private after the comma:

and complete the example, checking whether there is still the residue:

Decimal decimal fraction on the usual number

Decimal fraction, as we know consists of a whole and fractional part. When dividing decimal fractions to the usual number, first of all, it is necessary:

• split the whole part of the decimal fraction on this number;
• after the whole part is divided, you need to immediately put a comma in a private immediately and continue the calculation as in the usual division.

For example, we divide 4.8 to 2

We write this example to the corner:

Now we divide the whole part on 2. Four divided into two will be two. We write down the two in private and immediately put the comma:

Now I multiply the private on the divider and see whether there is a belt from division:

4-4 \u003d 0. The residue is zero. Zero not yet written, because the solution is not completed. Next, continue to calculate as in the usual division. Demolish 8 and divide it on 2

8: 2 \u003d 4. Record the fourth in private and immediately multiply it on the divider:

Received a response 2.4. The value of 4.8: 2 expression is 2.4

Example 2. Find an expression value 8.43: 3

We divide 8 to 3, we get 2. Immediately put the comma after twos:

Now I multiply the private on the divider of 2 × 3 \u003d 6. We write a six-eight seventh and find the residue:

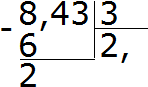
We divide 24 to 3, we get 8. Record the eight in private. Immediately multiply it on the divider to find the balance of division:

24-24 \u003d 0. The residue is zero. Zero not yet written. We demolish the last three of the divide and divide to 3, we get 1. Immediately multiply 1 to 3 to complete this example:

Received the answer 2.81. Means the value of expression 8.43: 3 is 2.81

Decimal decimal fraction for decimal fraction

To divide the decimal fraction to the decimal fraction, it is necessary to transfer comma to the right to the same number in a divider, and then they are after the comma in the divider, and then make division to the usual number.

For example, we divide 5.95 by 1.7

We write this expression

Now in divide and in the divider, we will move the comma to the right to the same number as they are after the comma in the divider. In the divider after a comma one digit. So we must in divide and in the divider move the comma to the right to one digit. Transfer:

After transferring the comma to the right to one digit, the decimal fraction 5,95 turned into a shot 59.5. And the decimal fraction 1.7 after the transfer of the comma to the right to one digit appealed to the usual number 17. And how to share the decimal fraction to the usual number we already know. Further computation is not much difficult:

The comma is transferred to the right to facilitate division. This is allowed due to the fact that when multiplying or dividing the divide and divider on the same number, the private does not change. What does it mean?

This is one of interesting features division. It is called the property of private. Consider the expression 9: 3 \u003d 3. If in this expression, the divider and divider multiply or divided into one and the same number, then the private 3 will not change.

Let's multiply divide and divider for 2, and let's see what happens from this:

(9 × 2): (3 × 2) \u003d 18: 6 \u003d 3

As can be seen from the example, the private has not changed.

The same thing happens when we transfer the comma in Delim and in the divider. In the previous example, where we divided 5.91 by 1.7, we were transferred in divide and divider to the comma on one digit to the right. After the transfer of the comma, the shot 5.91 was transformed into a fraction 59.1 and the fraction 1.7 was transformed into a normal number 17.

In fact, in this process, multiplication took place at 10. That's how it looked:

5.91 × 10 \u003d 59.1

Therefore, on the number of numbers after the comma in the divider, it depends on what the divider and divider will be multiplied. In other words, on the number of numbers after a comma in the divider, it will depend on how many numbers in the division and in the comma divider will be transferred to the right.

Decimal decimal fraction 10, 100, 1000

The division of decimal fractions on 10, 100, or 1000 is carried out in the same way as. For example, we split 2.1 to 10. I will solve this example:

But there is a second way. He is more easy. The essence of this method is that the comma in division is transferred to the left of so many numbers as zeros in the divider.

I decide the previous example in this way. 2.1: 10. We look at the divider. We are interested in how much zeros in it. We see that there is one zero. So in Delima 2.1 you need to move the comma to the left per digit. We transfer the comma to the left to one digit and see that there are no more numbers left. In this case, in front of the digit, add another zero. In the end we get 0.21

Let's try to divide 2.1 per 100. Among the 100 two zero. So in Delim 2.1 it is necessary to transfer the comma to the left into two digits:

2,1: 100 = 0,021

Let us try to divide 2.1 per 1000. Among 1000 three zero. So in Delima 2.1 it is necessary to transfer the comma to the left of three digits:

2,1: 1000 = 0,0021

Decision decimal fraction 0.1, 0,01 and 0.001

Decision decimal fraction 0.1, 0.01, and 0.001 is carried out in the same way as. In Delim and in the divider, you need to transfer the comma to the right to so many numbers as they are after the comma in the divider.

For example, we divide 6.3 to 0.1. First of all, we will transfer commas in divide and in the divider to the right on the same number as they are after the comma in the divider. In the divider after a comma one digit. So we transfer commas in divide and in the divider to the right to one digit.

After transferring the comma to the right to one digit, the decimal fraction 6.3 turns into a normal number 63, and the decimal fraction 0.1 after transferring the comma to the right to one digit turns into one. And divided 63 to 1 is very simple:

So the value of expression 6.3: 0,1 is 63

But there is a second way. He is more easy. The essence of this method is that the comma in division is transferred to the right to so many numbers as zeros in the divider.

I decide the previous example in this way. 6.3: 0.1. We look at the divider. We are interested in how much zeros in it. We see that there is one zero. So in divide 6.3 you need to transfer the comma to the right to one digit. We carry the comma to the right to one digit and get 63

Let us try to divide 6.3 to 0.01. In the divider 0.01 two zero. So in divide 6.3 it is necessary to transfer the comma to the right into two digits. But in division after the comma, only one digit. In this case, at the end you need to add one more zero. As a result, we get 630

Let's try to divide 6.3 to 0.001. In the divider 0.001 three zero. So in divide 6.3 it is necessary to transfer the comma to the right to three digits:

6,3: 0,001 = 6300

Tasks for self-decisions

Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons

Back forward

Attention! Preview slides is used exclusively for informational purposes and may not provide ideas about all presentation capabilities. If you are interested in this work, please download the full version.

The purpose of the lesson:

• In a fascinating form, introduce students to the rule of multiplication of decimal fraction on a natural number, on the discharge unit and the rule of expression of the decimal fraction as a percentage. Develop the ability to apply the knowledge gained when solving examples and tasks.
• Develop and activate logical thinking of students, the ability to identify regularities and generalize them, strengthen memory, the ability to cooperate, assist, evaluate their work and work each other.
• Rail interest in mathematics, activity, mobility, skill to communicate.

Equipment: Interactive board, poster with a digitalogram, posters with mathematician statements.

During the classes

1. Organizing time.
2. The oral account is a generalization of early material studied, preparation for the study of a new material.
3. Explanation of the new material.
4. Task at home.
5. Mathematical physical attachment.
6. Generalization and systematization of the knowledge gained in gaming form With the help of a computer.
7. Estimation.

2. Guys, today our lesson will be somewhat unusual, because I will spend it not alone, but with my friend. And my friend is also unusual, now you will see it. (Computer-cartoon appears on the screen). My friend has a name and he knows how to talk. What is your name, friend? The composhes replies: "My name is a composh." Are you ready to help me today? YES! Well, then let's start a lesson.

Today I came the encrypted digitalogram, the guys, which we must decide together and decipher. (A poster is hanging on the board with an oral account for the addition and subtraction of decimal fractions, as a result of the decision of which the guys receive the following code. 523914687. )

5	2	3	9	1	4	6	8	7
1	2	3	4	5	6	7	8	9

Decipher the received code helps a composh. As a result of the decoding, the word multiplication is obtained. Multiplication is keyword Topics of today's lesson. The lesson theme is displayed on the monitor: "Multiplying decimal fraction on a natural number"

Guys, we know how multiplication of natural numbers is performed. Today we will consider multiplication decimal numbers on a natural number. The multiplication of the decimal fraction on a natural number can be viewed as the sum of the terms, each of which is equal to this decimal fraction, and the number of components is equal to this natural Number. For example: 5,21 · 3 \u003d 5.21 + 5, 21 + 5,21 \u003d 15.63So, 5,21 · 3 \u003d 15.63. Representing 5.21 in the form of ordinary fraci on a natural number, we get

And in this case, the same result was 15.63. Now, not paying attention to the comma, we take the number 521 and change to this natural number instead of the number. Here we must remember that in one of the mill multipliers moved by two categories to the right. When multiplying numbers 5, 21 and3, we get a product equal to 15.63. Now in this example, the comma will move to the left for two discharge. Thus, how many times one of the multipliers increased, the work decreased in so many times. Based on similar moments of these methods, we conclude.

To multiply the decimal fraction on the natural number, it is necessary:
1) not paying attention to the comma, to perform multiplication of natural numbers;
2) In the resulting product, to separate the comma to the right of so many signs as they are in the decimal fraction.

The following examples are displayed on the monitor, which we disassemble with the composhes and guys: 5.21 · 3 \u003d 15.63 and 7.624 · 15 \u003d 114.34. After showing multiplication on a round number 12.6 · 50 \u003d 630. Next, I turn to the multiplication of the decimal fraction on the discharge unit. Show the following examples: 7,423 · 100 \u003d 742.3 and 5.2 · 1000 \u003d 5200. So, we enter the rule of multiplication of the decimal fraction on the discharge unit:

To multiply the decimal fraction on the discharge units 10, 100, 1000, etc., it is necessary in this fraction to move the comma to the right to so many signs as zeros in the record of the discharge unit.

I finish the explanation of the expression of the decimal fraction in percent. I enter the rule:

To express a decimal fraction in percent, it is necessary to multiply to 100 and attribute a sign%.

I cite an example on a computer 0.5 · 100 \u003d 50 or 0.5 \u003d 50%.

4. At the end of the explanation I give the guys homeworkwhich is also highlighted on the computer monitor: № 1030, № 1034, № 1032.

5. In order for the guys a little rest, we make a mathematical physical attachment to consolidate the themes. Everyone get up, I show the class solved examples and they must answer, correctly or not solved the example. If the example is solved correctly, then they raise their hands above their heads and make cotton palms. If the example is decided not true, the guys pull their hands to the side and knead the fingers.

6. And now you have a little rested, you can solve the tasks. Open the tutorial on page 205, № 1029. In this task, it is necessary to calculate the value of expressions:

Tasks appear on the computer. As they solve them, the picture appears with the image of the ship, which is floating with complete assembly.

No. 1031 Calculated:

Solving this task on the computer, gradually folds the rocket, deciding the last example, the rocket flies. The teacher makes small information to students: "Every year with the Kazakhstan land from the cosmodrome, Baikonur takes off to the stars of space ships. Next to Baikonur, Kazakhstan builds his new cosmodrome "Baiterek".

№ 1035. Task.

What distance will be passed in 4 hours, if the speed of the passenger car is 74.8 km / h.

This task is accompanied by a sound design and a summary problem on the monitor. If the task is solved, right, then the car begins to move forward to the finishing check box.

№ 1033. Write down decimal fractions in percent.

0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.

Solving each example, the letter appears when the answer appears, as a result of which the word appears Well done.

The teacher asks for a composite, why would this word appear? The composhes replies: "Well done guys!" And says goodbye to everyone.

The teacher sums up the lesson and estimates.

To understand how to multiply decimal fractions, consider specific examples.

The rule of multiplication of decimal fractions

1) Multiply, not paying attention to the comma.

2) As a result, we separate after the semicolons as many numbers as they are after the commas in both multipliers together.

Examples.

Find a product of decimal fractions:

To multiply decimal fractions, multiply, not paying attention to the commas. That is, we multiply not 6.8 and 3,4, but 68 and 34. As a result, we separate after the semicolons as many numbers as they are after the commas in both factors together. In the first factory after the semicolons, one figure, in the second, is also alone. In total, we separate the two digits after the comma. In the way, the final answer was obtained: 6.8 ∙ 3,4 \u003d 23.12.

We multiply decimal fractions, without taking into account the comma. That is, in fact, instead of multiplying 36.85 per 1.14, we multiply 3685 by 14. We get 51590. Now, in this result, it is necessary to separate the semicolons as many numbers as they are in both multipliers together. In the first number after the comma, two digits, in the second one. Total, separating the semicolons three numbers. Since in the end of the record after the comma, there is zero, in response we do not write it: 36.85 ∙ 1,4 \u003d 51.59.

To multiply these decimal fractions, multiply the numbers, not paying attention to the commas. That is, we multiply natural numbers 2315 and 7. We get 16205. In this number, it is necessary to separate four digits after the comma - as much as they are in both multipliers together (in each one - two). Ultimate answer: 23,15 ∙ 0.07 \u003d 1,6205.

The multiplication of the decimal fraction on the natural number is performed similarly. We multiply the numbers, not paying attention to the comma, that is, 75 multiply on 16. In the result resulting after the comma, there should be as many signs as they are in both multipliers together - one. Thus, 75 ∙ 1,6 \u003d 120.0 \u003d 120.

The multiplication of decimal fractions begin with the fact that we multiply natural numbers, as they do not pay attention to the commas. After that, we separate after the semicolons as many numbers as they are in both multipliers together. In the first number after the comma, two signs, in the second - also two. Total, as a result of the comma, four digits should stand: 4.72 ∙ 5.04 \u003d 23,7888.

Go to the study of the following action with decimal fractions, now we will comprehensively consider multiplying decimal fractions. First discuss general principles Multiples of decimal fractions. After that, we turn to the multiplication of the decimal fraction for a decimal fraction, we will show how the multiplication of decimal fractions is performed, consider solving examples. Then we will analyze the multiplication of decimal fractions on natural numbers, in particular 10, 100, etc. In conclusion, let's talk about multiplication of decimal fractions on ordinary fractions and mixed numbers.

Immediately, let's say that in this article we will only talk about multiplying positive decimal fractions (see positive and negative numbers). The remaining cases are disassembled in articles multiplication of rational numbers and multiplying valid numbers.

Navigating page.

General principles of multiplication of decimal fractions

Let us discuss the general principles that should be adhere to when making multiplication with decimal fractions.

Since the final decimal fractions and endless periodic fractions are a decimal form of recording ordinary fractions, the multiplication of such decimal fractions is essentially multiplying ordinary fractions. In other words, multiplying finite decimal fractions, multiplying finite and periodic decimal fractions, as well as multiplication of periodic decimal fractions It comes down to the multiplication of ordinary fractions after the translation of decimal fractions into ordinary.

Consider examples of the application of the voiced principle of multiplication of decimal fractions.

Example.

Perform multiplication of decimal fractions 1.5 and 0.75.

Decision.

Replace multiply decimal fractions with appropriate ordinary fractions. Since 1.5 \u003d 15/10 and 0.75 \u003d 75/100, then. It is possible to reduce the fraction, after which it is possible to separate the whole part of the incorrect fraction, and it is more convenient to record the resulting ordinary fraction 1 125/1 000 in the form of a decimal fraction 1,125.

Answer:

1.5 · 0.75 \u003d 1,125.

It should be noted that the final decimal fractions are conveniently multiplied by the Stage, we will talk about this method of multiplying decimal fractions.

Consider an example of multiplying periodic decimal fractions.

Example.

Calculate the product of periodic decimal fractions 0, (3) and 2, (36).

Decision.

Perform the translation of periodic decimal fractions into ordinary fractions:

Then. You can get an ordinary fraction to translate into a decimal fraction:

Answer:

0, (3) · 2, (36) \u003d 0, (78).

If there are infinite non-periodic fractions among the multiply decimal fractions, then all the multiplied fractions, including finite and periodic, should be rounded to a certain discharge (see rounding numbers), After that, to perform multiplication of the final decimal frains obtained after rounding.

Example.

Perform multiplication of decimal fractions 5,382 ... and 0.2.

Decision.

At first rounded the infinite non-periodic decimal fraction, rounding can be carried out to the hundredths, we have 5.382 ... ≈5.38. The final decimal fraction 0.2 rounded to the hundredths is not necessary. Thus, 5.382 ... · 0.2≈5.38 · 0.2. It remains to calculate the product of finite decimal fractions: 5.38 · 0.2 \u003d 538/100 · 2/10 \u003d 1 076/1 000 \u003d 1.076.

Answer:

5.382 ... · 0.2≈1.076.

Multiplying decimal fractions

The multiplication of finite decimal fractions can be performed by a column, similar to multiplication of a column of natural numbers.

Formulate the rule of multiplication of decimal fractions of the column. To multiply decimal strobs, it is necessary:

• not paying attention to the commas, to perform multiplication by all the rules of multiplication of the column of natural numbers;
• in the resulting number, to separate the decimal point as many digits to the right, how many decimal signs in both multipliers together, while in the work there is not enough digits, then you need to add the right amount zeros.

Consider examples of multiplication of decimal fractions of the column.

Example.

Perform multiplication of decimal fractions 63.37 and 0.12.

Decision.

Let's give multiplication of decimal fractions by the column. First, multiply the numbers, not paying attention to the commas:

It remains in the resulting product to put a comma. She needs to separate 4 digits to the right, as in the multipliers in the amount of four decimal signs (two in fractions 3.37 and two in fractions 0.12). There are enough digits there, so the zeros will not add to the left. We will finish the record:

As a result, we have 3.37 · 0.12 \u003d 7.6044.

Answer:

3.37 · 0.12 \u003d 7.6044.

Example.

Calculate the product of decimal fractions 3,2601 and 0.0254.

Decision.

After making a multiplication by a column excluding commas, we get the following picture:

Now in the work it is necessary to separate the semicolons 8 digits to the right, since the total number of decimal signs of multiplying fractions is equal to eight. But in the work only 7 digits, therefore, you need to put as much zeros on the left so that you can separate the semicolons 8 digits. In our case, you need to assign two zero:

On this multiplication of decimal fractions, the column is completed.

Answer:

3,2601 · 0.0254 \u003d 0.08280654.

Multiplication of decimal fractions by 0.1, 0.01, etc.

Quite often has to multiply decimal fractions by 0.1, 0.01 and so on. Therefore, it is advisable to formulate a rule of multiplication of decimal fraction for these numbers, which follows from the principles of multiplication of decimal fractions discussed above.

So, multiplication of this decimal fraction 0.1, 0.01, 0.001 and so on gives a fraction that is obtained from the original, if you transfer the comma to the left to 1, 2, 3 and so on the digits, respectively, while not enough for the transfer of the semicolon, then you need to leave on the left required amount zeros.

For example, to multiply the decimal fraction 54.34 by 0.1, it is necessary to transfer the comma to the left to the left to 1 digit to move the comma to the left, and it turns out the shot 5,434, that is, 54.34 · 0.1 \u003d 5,434. We give another example. Multiply decimal fraction 9.3 to 0.0001. To do this, we need a multiply decimal fraction 9.3 to move the comma on 4 digits to the left, but the entry of the fraction 9.3 does not contain such a number of characters. Therefore, we need to record the fraction 9.3 on the left to attribute so much zeros so that you can easily carry out a comma transfer by 4 digits, we have 9.3 · 0.0001 \u003d 0.00093.

Note that the announced rule of multiplication of decimal fraction 0.1, 0.01, ... rightly for infinite decimal fractions. For example, 0, (18) · 0.01 \u003d 0.00 (18) or 93.938 ... · 0.1 \u003d 9,3938 ....

Multiplication of decimal fraction on a natural number

In its essence multiplying decimal fractions on natural numbers It does not differ from the multiplication of the decimal fraction for a decimal fraction.

The final decimal fraction is multiplied by a natural number more convenient than the column, while the rules of multiplication of the decimal fraction, discussed in one of the preceding paragraphs.

Example.

Calculate the product 15 · 2.27.

Decision.

We will spend multiplication of a natural number for a decimal fraction of a column:

Answer:

15 · 2.27 \u003d 34.05.

When multiplying a periodic decimal fraction on a natural number, a periodic fraction should be replaced by an ordinary fraction.

Example.

Multiply decimal fraction 0, (42) to a natural number 22.

Decision.

First, we will transfer a periodic decimal fraction in an ordinary fraction:

Now perform multiplication :. This result in the form of a decimal fraction has a form 9, (3).

Answer:

0, (42) · 22 \u003d 9, (3).

And when multiplying an infinite non-periodic decimal, the fraction on a natural number must be rounded.

Example.

Perform multiplication 4 · 2.145 ....

Decision.

Rounding to the hundredths The initial infinite decimal fraction, we will come to the multiplication of the natural number and the final decimal fraction. We have 4 · 2,145 ... ≈4 · 2.15 \u003d 8.60.

Answer:

4 · 2,145 ... ≈8.60.

Multiplying decimal fraction 10, 100, ...

Quite often has to multiply decimal fractions by 10, 100, ... Therefore, it is advisable to stay in detail in these cases.

Sound the rule of multiplication of decimal fraction 10, 100, 1,000, etc. When multiplying decimal fractions 10, 100, ... in its records you need to transfer the comma to the right to 1, 2, 3, ... numbers, respectively and discard the extra zeros on the left; If there is not enough digits in the recording of a multiplying fraction, then you need to add the required number of zeros to the right.

Example.

Multiply decimal fraction 0.0783 per 100.

Decision.

We transfer into records of the fraction 0.0783 into two digits to the right, while we get 007.83. Throwing two zero on the left, we get a decimal fraction 7.38. Thus, 0.0783 · 100 \u003d 7.83.

Answer:

0.0783 · 100 \u003d 7.83.

Example.

Perform multiplication of decimal fraction 0.02 to 10,000.

Decision.

To multiply 0.02 by 10,000, we need to move the comma to 4 digits to the right. Obviously, in the entry of the fraction 0.02, there are not enough digits to transfer a comma to 4 digits, so I add a few zeros to the right so that you can transfer the comma. In our example, it is enough to add three scratch, we have 0.02000. After transferring the comma, we get recording 00200.0. Throwing the zeros on the left, we have a number 200.0, which is equal to a natural number 200, it is the result of multiplication of decimal fraction 0.02 to 10,000.

§ 107. Addition of decimal fractions.

The addition of decimal fractions is performed in the same way as the addition of integers. Let's make sure of this on the examples.

1) 0.132 + 2.354. Let's sign the components one below the other.

Here, from adding 2 thousandths with 4 thousands, it turned out 6 thousandths;
the addition of 3 hundredths with 5 hundredths turned out to be 8 hundredths;
from adding to 1 tenth with 3 tenth -4 tenths and
frequently with 2 whole - 2 integers.

2) 5,065 + 7,83.

In the second term there are no thousandths, so it is important to prevent errors when signing the components of each other.

3) 1,2357 + 0,469 + 2,08 + 3,90701.

Here, when adding thousandth fractions, 21 thousandths turned out; We wrote 1 under the thousandths, and 2 added to the hundredth, thus, in the discharge of hundredths, we turned out the following terms: 2 + 3 + 6 + 8 + 0; In sum, they give 19 hundredths, we signed 9 under the hundredths, and 1 were submitted to the tenth, etc.

Thus, when adding decimal fractions, the following order should be observed: the fraction is to sign one under the other way that in all the components of the same discharges were in each other and all commas stood in the same vertical column; At the right of the decimal signs of some of the terms are attributed, at least mentally, such a number of zeros so that all the lifetimes have had the same number of numbers. Then perform the addition of discharges, starting on the right side, and in the resulting amount they put a comma in the same vertical column, in which it is in the data of the terms.

§ 108. Subtraction of decimal fractions.

Deduction of decimal fractions is performed in the same way as the subtraction of integers. Show it on the examples.

1) 9.87 - 7.32. Subscribe subtractable under reduced so that the units of one discharge are each other:

2) 16.29 - 4.75. Subscribe subtracted under the reduced, as in the first example:

To make the deduction of the tenths, it was necessary to take one entire unit from 6 and crush it into tenths.

3) 14,0213- 5,350712. Subscribe subtracted under the dimming:

The subtraction was performed as follows: since we cannot subtract 2 million out of 0, then you should contact the nearest discharge, standing on the left, that is, it is also worth a zero on the place of the hundreds, so we take from 3 ten thousand ten years old and We crush it into the hundreds, we obtain 10 hundreds of thousands, of which 9 hundreds are left in the discharge of hundreds of thousands, and 1 hundreds of discharge in millions, we get 10 million. Thus, in the three recent categories, we turned out: Millionnaya 10, hundredsmaking 9, ten-thousand 2. These numbers are for greater clarity and convenience (so as not to forget) are recorded from above above the corresponding fractional discharges of the reduced. Now you can proceed to subtract. Out of 10 million, we subtract 2 million, we get 8 million; From 9 hundreds, we subtract 1 hundredsmaking, we get 8 hundreds and so on.

Thus, when subtracting decimal fractions, the following order is observed: signed subtractable under reduced so that the same discharges are in each other and all commas stood in the same vertical column; The right is attributed to at least mentally, in a decreasing or deductable so much zeros so that they have the same number of digits, then subtracting the discharges, starting on the right side, and in the resulting difference they put a comma in the same vertical column, in which it is in Reduced and subtracted.

§ 109. Multiplication of decimal fractions.

Consider several examples of multiplication of decimal fractions.

To find the product of these numbers, we can argue as follows: if the multiplier is increased 10 times, then both of the factors will be whole numbers and we can multiply them according to the rules of multiplying integers. But we know that with an increase in one of the factors, a few times the work increases at the same time. It means that the number that will succeed on multiplying whole factors, i.e. 28 by 23, 10 times more than the true work, and to get a true work, a found work is required to reduce 10 times. Consequently, here you have to perform a multiplication of 10 and once a division of 10, but multiplication and division by 10 is carried out by transferring the comma to the right and left to one sign. Therefore, it is necessary to do this: in the multiplier to transfer the comma to the right to one sign, it will be equal to 23, then you need to multiply the integers obtained:

This work is 10 times more true. Consequently, it must be reduced 10 times, for which we will move the comma for one sign to the left. Thus, we get

28 2,3 = 64,4.

In order to check, you can write a decimal to write with the denominator and perform an action according to the rule of multiplication of ordinary fractions, i.e.

2) 12,27 0,021.

The difference of this example from the previous one is that both factors are represented by decimal fractions. But here in the process of multiplication will not pay attention to the commas, i.e., temporarily increase the multiplier 100 times, and the multiplier of 1,000 times, which is why the work will increase 100,000 times. Thus, multiplying 1,227 to 21, we get:

1 227 21 = 25 767.

Considering that the resulting work is 100,000 times more true, we must now reduce it 100,000 times by appropriate decisions in it, then we get:

32,27 0,021 = 0,25767.

Check:

Thus, in order to multiply two decimal fractions, it is sufficient, not paying attention to the commas, multiply them as integers and in the work to separate the comma on the right side as many decimal signs as they were in the multiplier and in the multiplier together.

In the last example, a work was made with five decimal signs. If such a big accuracy is not required, then rounding decimal fraction is done. When rounding, the rule should be used as it was indicated for integers.

§ 110. Multiplication with tables.

The multiplication of decimal frains can sometimes be performed using tables. For this purpose, you can, for example, use those multiplication tables. two-digit numbers, the description of which was given earlier.

1) Multiply 53 by 1.5.

We will multiply 53 to 15. In the table, this product is 795. We found a work 53 to 15, but we have a second factor 10 times less, it means that the work should be reduced by 10 times, i.e.

53 1,5 = 79,5.

2) Multiply 5.3 per 4.7.

First, we will find the work table 53 to 47 in the table, it will be 2,491. But since we have increased the multiplier and multiplier of a total of 100 times, then the resulting product is 100 times more than it follows; Therefore, we must reduce this work 100 times:

5,3 4,7 = 24,91.

3) Multiply 0.53 by 7.4.

First, we will find the work table 53 at 74; It will be 3 922. But since we increased the multiplier 100 times, and the multiplier is 10 times, then the work increased 1,000 times; Therefore, we must now reduce it 1,000 times:

0,53 7,4 = 3,922.

§ 111. The division of decimal trips.

Decision decimal fractions We will consider in this order:

1. division decimal fraction for an integer

1. Dividing decimal fraction for an integer.

1) We divide 2.46 to 2.

We divided into 2 first integers, then tenths and, finally, hundredths.

2) We divide 32.46 to 3.

32,46: 3 = 10,82.

We divided 3 tens of 3, then we began to divide 2 units by 3; Since the number of divide (2) units is less than the divider (3), it was necessary to put 0 in private; Further, we demolished 4 tenths to the residue and divided 24 tenths to 3; They received in private 8 tents and, finally, divided 6 hundredths.

3) We divide 1.2345 to 5.

1,2345: 5 = 0,2469.

Here, in the first place, there was a zero of whole, since one whole is not divided into 5.

4) We divide 13.58 to 4.

The peculiarity of this example is that when we received in private 9 hundredths, then a residue was revealed equal to 2 hundredth, we crushed the remainder of the residue to thousands of thousands, received 20 thousand and brought the division to the end.

Rule.The division of the decimal fraction is performed in the same way as the division of integers, and the resulting residues turn into decimal shares, more and smaller; The division continues until the residue is zero.

2. The division of the decimal fraction for a decimal fraction.

1) We divide 2.46 to 0.2.

We already know how to share the decimal fraction for an integer. Think if it is impossible and this new case of division is reduced to the previous one? At one time, we considered the wonderful property of the private, which remains unchanged while simultaneously increasing or decreasing a divide and divider in the same number of times. We can easily fulfill the division of the numbers offered to us if the divider was an integer. To do this, it is enough to increase it 10 times, and to obtain the right private, it is necessary for the same time, that is, 10 times, increase and delimitable. Then dividing these numbers will be replaced by dividing such numbers:

and no amendments in private do no longer have to do.

Perform this division:

So, 2.46: 0.2 \u003d 12.3.

2) We divide 1.25 per 1.6.

We increase the divider (1.6) 10 times; so that the private has not changed, increase 10 times and divisible; 12 is not divided into 16, so we write in private 0 and divide 125 tenths to 16, we get in the private 7 tenths and in the residue 13. we split 13 tenths in the hundredths by tinting zero and divide 130 hundredths to 16, etc. Pay attention Next:

a) when it does not work in private, then they write zero in their place;

b) when after demolitioning to the residue, the divisory numbers turns out a number that is not divided into the divider, it is written in private;

c) when after the demolition of the last digit divide, it does not end, then, attributing to the remnants of zeros, continue division;

d) if divisible is an integer, then when dividing it for a decimal fraction, it is carried out by attributing to it zeros.

Thus, in order to divide the number for a decimal fraction, you need to discard the comma in the divider, and then increase the divider in so many times, as much as the divider has increased when the semicolon has dropped, after which the division according to the decimal decimation rule for an integer.

§ 112. Approached private.

In the previous paragraph, we looked at the division of decimal fractions, and in all the examples solved by us, the division was made to the end, that is, the exact private one was obtained. However, in most cases, the exact private cannot be obtained, no matter how far we continued division. Here is one of these cases: we divide 53 per 101.

We have already received five digits in private, and the division has not yet completed and there is no hope that it will ever end, because in the remnants we begin to appear numbers that have met already. In particular, the number will also be repeated: it is obvious that following the number 7, a digit 5 \u200b\u200bwill appear, then 2, etc. without end. In such cases, division is interrupted and limited to several first numbers of private. Such private is called approximate. As it is necessary to perform division, we will show on the examples.

Let it take 25 divided by 3. It is obvious that an accurate private, expressed integer or decimal fraction, cannot happen from such a division. Therefore, we will look for an approximate private:

25: 3 \u003d 8 and residue 1

Approximate private equal to 8; It, of course, is less than exact private, because there is a residue 1. To get accurate private, you need to the found approximate private, i.e. K 8, add a fraction that will result from dividing the residue equal to 1, by 3; It will fraction 1/3. It means that the exact private will express the mixed number 8 1/3. Since 1/3 is the correct fraction, that is, the fraction, smaller units, then throwing it away, we will admit errorthat less one. Private 8 will be an approximate private with an accuracy of a unit with a disadvantage. If we, instead of 8, take in private 9, then also let's accept the error that is less than the unit, since we will add not a whole unit, A 2/3. Such a private will an approximate private with an accuracy of the unit with an excess.

We are now another example. Let it take 27 divided by 8. Since it will not be exactly the exact private, pronounced integer, then we will look for an approximate private:

27: 8 \u003d 3 and residue 3.

Here the error is 3/8, it is less than one, it means that the approximate private (3) is found with an accuracy of the unit with a disadvantage. We continue division: split the residue 3 in tenths, we get 30 tenths; We divide them by 8.

We got in private at the place of the tenth 3 and in the residue of the tenths. If we are in a private quantitative number of 3.3, and the remainder of 6 will throw, then we will admit an error that is less than one tenth. Why? Because the exact private would have happened when we would add to 3.3 another result of dividing 6 tenths by 8; From this division would be 6/80, which is less than one tenth. (Check!) Thus, if in private we limit ourselves to tenth shares, then you can say that we found private up to one tenth(With disadvantage).

Continue division to find another decimal sign. To do this, we will split 6 tenths in hundredths and we get 60 hundredths; We divide them by 8.

In the private in third place it turned out 7 and in the residue of 4 hundredths; If we throw them, then the error is less than one hundredth, because 4 hundredths divided by 8 are less than one hundred. In such cases, it is said that private found with an accuracy of one hundred (With disadvantage).

In the example, which we now consider, you can get an accurate private, expressed by a decimal fraction. To do this, the last remainder, 4 hundredths, crush into the thousands and perform division by 8.

However, in the vast majority of cases, it is impossible to obtain accurate private and has to be limited to its approximated values. We now consider this example:

40: 7 = 5,71428571...

The points set at the end of the number indicate that the division is not completed, i.e. the equality is approximate. Usually, approximate equality is recorded like this:

40: 7 = 5,71428571.

We took a private with eight decimal signs. But if such a big accuracy is not required, it is possible to limit ourselves to the whole part of the private, i.e. Number 5 (more precisely 6); For greater accuracy, we could take into account the tenths and take a private equal to 5.7; If this accuracy is also insufficient, then you can stay at hundredths and take 5.71, etc. We will write separate private and call them.

The first approximate private with an accuracy of 6.

Second "" "up to one tenth 5.7.

Third "" "up to one hundred 5.71.

Fourth "" "to one thousandth 5,714.

Thus, to find an approximate private with accuracy to some, for example, the 3rd decimal sign (i.e. to one thousandth), the division is stopped as soon as this sign is found. At the same time, you need to remember the rule set out in § 40.

§ 113. The simplest tasks for interest.

After studying decimal fractions, we will decide some more interest tasks.

These tasks are similar to what we solved in the department of ordinary fractions; But now hundredth lobes we will be recorded in the form of decimal fractions, i.e. without a clearly designated denominator.

First of all, you need to be able to easily move from an ordinary fraction to decimal with a denominator 100. For this, the numerator should be divided into the denominator:

The table below shows how the number with the% icon (percentage) is replaced with a decimal fraction with a denominator 100:

Consider now several tasks.

1. Finding percent of this number.

Task 1.Only 1,600 people live in one village. Number of children school age is 25% of total residents. How many school children in this village?

In this task you need to find 25%, or 0.25, from 1 600. The task is solved by multiplication:

1 600 0.25 \u003d 400 (children).

Consequently, 25% of 1,600 is 400.

For a clear understanding of this task, it is useful to recall that each hundred people account for 25 school children. Therefore, in order to find the number of all children of school age, you can first find out how many hundreds of 1,600 (16), and then 25 multiply by the number of hundreds (25 x 16 \u003d 400). This way you can check the validity of the solution.

Task 2. Savings tickets give depositors annually 2% of income. How much income in the year will receive the investor, putting on the box office: a) 200 rubles.? b) 500 rubles.? c) 750 rubles.? d) 1000rub.?

In all four cases, to solve the problem, it will be necessary to calculate 0.02 from the specified sums, i.e. each of these numbers will have to multiply by 0.02. Let's do it:

a) 200 0.02 \u003d 4 (rub.),

b) 500 0.02 \u003d 10 (rub.),

c) 750 0.02 \u003d 15 (rub.),

d) 1 000 0.02 \u003d 20 (rub.).

Each of these cases can be verified by the following considerations. Savings cash registers give to depositors 2% of income, i.e. 0.02 from the amount due to the savings. If the amount was equal to 100 rubles, then 0.02 would be 2 rubles from her. So each hundred brings to the depositor of 2 rubles. income. Therefore, in each of the cases considered, it is enough to figure out how many hundreds in the number of hundreds and this number of hundreds of 2 rubles. In example, a) hundred 2, it means that

2 2 \u003d 4 (rub.).

In the example of d) hundred 10, it means that

2 10 \u003d 20 (rub.).

2. Finding a number by its percentages.

Task 1. The spring school has released 54 student, which is 6% of the total number of students. How many students were at school in the past school year?

We understand the meaning of this task first. The school released 54 student, which is 6% of the total number of students, or, in other words, 6 hundredths (0.06) from all students of the school. It means that we know part of students, expressed by the number (54) and the fraction (0.06), and on this fraction, we must find the entire number. Thus, we have an ordinary task for finding a number of fractions (§90 p. 6). The tasks of this type are solved by division:

It means that there were 900 students in school.

Such tasks are useful to check the inverse problem by solving, i.e., after solving the problem, at least in the mind, to solve the task of the first type (to find a percent of the number of this number): take the found number (900) for this and find the percentage indicated from it , namely:

900 0,06 = 54.

Task 2.Family spends 780 rubles for meals for a month, which is 65% of the monthly earnings of the Father. Determine its monthly earnings.

This task has the same meaning as the previous one. It gives a part of the monthly earnings, expressed in rubles (780 rubles), and it is indicated that this part is 65%, or 0.65, from all earnings. And the desired is all earnings:

780: 0,65 = 1 200.

Consequently, the desired earnings is 1200 rubles.

3. Finding the interest rate of numbers.

Task 1. In the school library only 6,000 books. Among them are 1,200 books in mathematics. How many percent of mathematical books make up from the number of all the books available in the library?

We have already considered (§97) of this kind of task and concluded that to calculate the percentage of two numbers, you need to find the ratio of these numbers and multiply it to 100.

Our task you need to find the percentage of numbers 1,200 and 6,000.

Find at first their attitude, and then multiply it at 100:

Thus, the percentage of numbers 1,200 and 6,000 is 20. In other words, mathematical books make up 20% of the total number of all books.

To check with a reference task: to find 20% of 6,000:

6 000 0,2 = 1 200.

Task 2.The plant should get 200 tons of coal. Already brought 80 tons. How many percent of coal delivered to the plant?

This task is asked how much percent one number (80) is from another (200). The ratio of these numbers will be 80/200. Multiply it at 100:

So, 40% of coal delivered.