Область визначення та область значень функції.В елементарній математиці вивчаються функції лише на безлічі дійсних чисел R.Це означає, що аргумент функції може набувати ті дійсні значення, у яких функція визначена, тобто. вона також набуває лише дійсних значень. Безліч Xвсіх допустимих дійсних значень аргументу x, при яких функція y= f(x)визначена, називається областю визначення функції. Безліч Yвсіх дійсних значень y, які приймає функція, називається областю значень функції. Тепер можна надати більш точне визначення функції: правило(закон) відповідності між множинами X та Y, за яким для кожного елемента з множиниX можна знайти один і тільки один елемент з множини Y, називається функцією.

З цього визначення випливає, що функція вважається заданою, якщо:

Задано область визначення функції X ;

Задано область значень функції Y ;

Відомо правило (закон) відповідності, причому таке, що для кожного

Значення аргументу можна знайти лише одне значення функції.

Ця вимога однозначності функції є обов'язковою.

Монотонна функція.Якщо для будь-яких двох значень аргументу x 1 та x 2 з умови x 2 > x 1 слід f(x 2) > f(x 1), то функція f(x) називається зростаючою; якщо для будь-яких x 1 та x 2 з умови x 2 > x 1 слід f(x 2) < f(x 1), то функція f(x) називається спадаючою. Функція, яка тільки зростає або лише зменшується, називається монотонної.

Обмежена та необмежена функції.Функція називається обмеженоюякщо існує таке позитивне число M, що | f(x) | Mдля всіх значень x.Якщо такого числа немає, то функція - необмежена.

Приміри.

Функція, зображена на рис.3 є обмеженою, але не монотонною. Функція на рис.4 - саме навпаки, монотонна, але необмежена. (Поясніть це, будь ласка!).

Безперервна та розривна функції.Функція y = f (x) називається безперервний у точціx = a, якщо:

1) функція визначена при x = a, Тобто. f (a) існує;

2) існує кінцевиймежа lim f (x) ;

x→a

(Див. «Межі функцій»)

3) f (a) = lim f (x) .

x→a

Якщо не виконується хоча б одна з цих умов, то функція називається розривнийу точці x = a.

Якщо функція безперервна в всіх точках своєї галузі визначення, то вона називається безперервною функцією.

Парна та непарна функції.Якщо для будь-якого x f(- x) = f (x), то функція називається парної;якщо має місце: f(- x) = - f (x), то функція називається непарний. Графік парної функції симетричний щодо осі Y(рис.5), a графік непарної функції цимметричний щодо початку координат(Рис.6).

Періодична функція.Функція f (x) - періодичнаякщо існує таке відмінне від нулячисло T, що для будь-якого xв галузі визначення функції має місце: f (x + T) = f (x). Таке найменшечисло називається періодом функції. Усі тригонометричні функції є періодичними.

П р і м е р 1 . Довести, що sin xмає період 2 .

Рішення. Ми знаємо, що sin ( x+ 2n) = sin x, де n= 0, ± 1, ± 2, …

Отже, додавання 2 nдо аргументу синуса не

Змінює його значення. Чи існує інше число з таким

А якістю?

Припустимо, що P- Таке число, тобто. рівність:

Sin ( x+ P) = sin x,

Справедливо для будь-якого значення x. Але тоді воно має

Місце і при x= / 2, тобто.

Sin (/ 2 + P) = sin / 2 = 1.

Але за формулою приведення sin (/2 + P) = cos P. Тоді

З двох останніх рівностей випливає, що cos P= 1, але ми

Знаємо, що це правильно лише за P = 2n. Оскільки найменшим

Відмінним від нуля числом із 2 nє 2, то це число

І є період sin x. Аналогічно доводиться, що 2з nє , таким чином, це період 2 x.

Нулі функції.Значення аргументу, у якому функція дорівнює 0, називається нулем (коренем) функції. Функція може мати кілька нулів. Наприклад, функція y = x (x + 1) (x-3) має три нулі: x= 0, x= -1, x= 3. Геометрично нуль функції - це абсциса точки перетину графіка функції з віссю Х .

На рис.7 представлений графік функції з нулями: x= a, x = bі x= c.

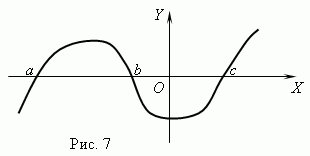
Асимптота.Якщо графік функції необмежено наближається до деякої прямої при віддаленні від початку координат, то ця пряма називається асимптотою.

Нулі функції
Нулем функції називається те значення х, при якому функція звертається до 0, тобто f(x)=0.

Нулі – це точки перетину графіка функції з віссю Ох.

Парність функції
Функція називається парною, якщо для будь-кого хз області визначення виконується рівність f(-x) = f(x)

Парна функція симетрична щодо осі Оу

Непарність функції
Функція називається непарною, якщо для будь-кого хз області визначення виконується рівність f(-x) = -f(x).

Непарна функція симетрична щодо початку координат.
Функція яка не є ні парною, ні непарною називається функцією загального вигляду.

Зростання функції
Функція f(x) називається зростаючою, якщо більшого значенняаргументу відповідає більше значення функції, тобто.

Зменшення функції
Функція f(x) називається спадною, якщо більшого значення аргументу відповідає менше значення функції, тобто.

Проміжки, на яких функція або лише зменшується, або тільки зростає, називаються проміжками монотонності. Функція f(x) має 3 проміжки монотонності:

Знаходять проміжки монотонності за допомогою сервісу Інтервали зростання та зменшення функції

Локальний максимум
Крапка х 0називається точкою локального максимуму, якщо для будь-якого хз околиці точки х 0виконується нерівність: f(x 0) > f(x)

Локальний мінімум
Крапка х 0називається точкою локального мінімуму, якщо для будь-якого хз околиці точки х 0виконується нерівність: f(x 0)< f(x).

Точки локального максимуму та точки локального мінімуму називаються точками локального екстремуму.

точки локального екстремуму

Періодичність функції
Функція f(x) називається періодичною, з періодом Т, якщо для будь-кого хвиконується рівність f(x+T) = f(x).

Проміжки знакостійності
Проміжки, у яких функція або лише позитивна, або лише негативна, називаються проміжками знакопостійності.

Безперервність функції
Функція f(x) називається безперервною в точці x 0 якщо межа функції при x → x 0 дорівнює значенню функції в цій точці, тобто. .

Точки розриву
Точки, в яких порушена умова безперервності, називаються точками розриву функції.

x 0- Точка розриву.

Загальна схема для побудови графіків функцій

1. Знайти область визначення функції D(y).

2. Знайти точки перетину графіка функцій з осями координат.

3. Дослідити функцію на парність чи непарність.

4. Дослідити функцію на періодичність.

5. Знайти проміжки монотонності та точки екстремуму функції.

6. Знайти проміжки опуклості та точки перегину функції.

7. Знайти асимптоти функції.

8. За наслідками дослідження побудувати графік.

Приклад:Дослідити функцію та побудувати її графік: y = x 3 – 3x

1) Функція визначена по всій числовій осі, тобто її область визначення D(y) = (-∞; +∞).

2) Знайдемо точки перетину з осями координат:

з віссю ОХ: розв'яжемо рівняння x 3 – 3x = 0

з віссю ОY: y(0) = 0 3 - 3 * 0 = 0

3) З'ясуємо, чи не є функція парної чи непарної:

y(-x) = (-x) 3 – 3(-x) = -x 3 + 3x = - (x 3 – 3x) = -y(x)

Звідси випливає, що функція є непарною.

4) Функція неперіодична.

5) Знайдемо проміжки монотонності та точки екстремуму функції: y' = 3x 2 - 3.

Критичні точки: 3x2 - 3 = 0, x2 = 1, x = ±1.

y(-1) = (-1) 3 – 3(-1) = 2

y(1) = 1 3 – 3*1 = -2

6) Знайдемо проміжки опуклості та точки перегину функції: y'' = 6x

Критичні точки: 6x=0, x=0.

y(0) = 0 3 - 3 * 0 = 0

7) Функція безперервна, асимптот у неї немає.

8) За результатами дослідження збудуємо графік функції.

Межі та безперервність

Безліч

Під безліччюрозуміється сукупність однорідних об'єктів. Об'єкти, які утворюють безліч, називаються елементамиабо точкамицієї множини. Безліч позначають великими літерами, які елементи – малими. Якщо aє елементом множини A, то використовується запис aÎ A. Якщо bне є елементом множини A, то це записується так: b Ï A. Безліч, яке містить жодного елемента, називається порожнім безліччю і позначається так: Ø.

Якщо безліч Bскладається з частини елементів множини Aабо збігається з ним, то безліч Bназивають підмножиноюмножини і позначають BÌ A.

Дві множини називають рівнимиякщо вони складаються з одних і тих же елементів.

Об'єднаннямдвох множин Aі Bназивається безліч C, Що складається з усіх елементів, що належать хоча б одному з множин: C=AÈ B.

Перетиномдвох множин Aі Bназивається безліч C, Що складається з усіх елементів, що належать кожному з даних множин: C=AÇ B.

Різницямножин Aі Bназивається безліч E A, які не належать безлічі B: .

Доповненнямбезлічі AÌ Bназивається безліч C, Що складається з усіх елементів множини B, що не належать A.

Багато, елементами яких є дійсні числа, називаються числовими:

При цьому NÌ ZÌ QÌ R, IÌ Rі R=IÈ Q.

Безліч X, елементи якого задовольняють нерівності називається відрізком(сегментом) і позначається [ a; b]; нерівності a<x<b – інтерваломі позначається (); нерівностям та - напівінтерваламита позначаються відповідно і . Також часто доводиться мати справу з нескінченними інтервалами та напівінтервалами: , , , і . Усі їх зручно називати проміжками .

Інтервал, тобто. безліч точок, що задовольняють нерівності (де ), називається околицею точки a.

Концепція функції. Основні властивості функції

Якщо кожному елементу xбезлічі Xставиться у відповідність єдиний елемент yбезлічі Y, то кажуть, що на безлічі Xзадана функція y=f(x). При цьому xназивають незалежної змінноїабо аргументом, а y – залежною змінноюабо функцією, а fпозначає закон відповідності. Безліч Xназивають областю визначенняфункції, а безліч Y – областю значеньфункції.

Існує кілька способів завдання функцій.

1) Аналітичний метод – функція задається формулою виду y=f(x).

2) Табличний спосіб – функція задається таблицею, що містить значення аргументу та відповідні їм значення функції y=f(x).

3) Графічний метод – зображення графіка функції, тобто. безлічі точок ( x; y) координатної площини, абсциси яких представляють значення аргументу , а ординати – відповідні значення функції y=f(x).

4) Словесний метод – функція описується правилом її складання. Наприклад, функція Діріхле набуває значення 1, якщо x– раціональне число та 0, якщо x- Ірраціональне число.

Вирізняють такі основні властивості функцій.

1 Парність та непарністьФункція y=f(x) називається парноїякщо для будь-яких значень xв галузі її визначення виконується f(–x)=f(x), і непарною, якщо f(–x)=–f(x). Якщо не виконується жодна з перелічених рівностей, то y=f(x) називається функцією загального вигляду. Графік парної функції симетричний щодо осі Ой, А графік непарної функції симетричний щодо початку координат.

2 МонотонністьФункція y=f(x) називається зростаючою (спадаючою) на проміжку Xякщо більшому значенню аргументу з цього проміжку відповідає більше (менше) значення функції. Нехай x 1 ,x 2 Î X, x 2 >x 1 . Тоді функція зростає на проміжку X, якщо f(x 2)>f(x 1), і зменшується, якщо f(x 2)<f(x 1).

Поряд із зростаючими та спадними функціями розглядають незменшуючі та незростаючі функції. Функція називається невпадаючою (незростаючою), якщо при x 1 ,x 2 Î X, x 2 >x 1 виконується нерівність f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).

Зростаючі та спадні функції, а також незростаючі та незменшувальні функції називають монотонними.

3 ОбмеженістьФункція y=f(x) називається обмеженою на проміжку Xякщо існує таке позитивне число M>0, що | f(x)|≤Mдля будь-кого xÎ X. У інакшефункція називається необмеженою на X.

4 ПеріодичністьФункція y=f(x) називається періодичною з періодом T≠0, якщо для будь-яких xз області визначення функції f(x+T)=f(x). Надалі під періодом будемо розуміти найменший позитивний період функції.

Функція називається явнийякщо вона задана формулою виду y=f(x). Якщо функція задана рівнянням F(x, y)=0, не дозволеним щодо залежної змінної y, то її називають неявний.

Нехай y=f(x) є функція від незалежної змінної , визначена на множині Xз областю значень Y. Поставимо у відповідність кожному yÎ Yєдине значення xÎ X, за якого f(x)=y. Тоді отримана функція x=φ (y), визначена на безлічі Yз областю значень X, називається зворотнійі позначається y=f –1 (x). Графіки взаємно зворотних функцій симетричні щодо бісектриси першої та третьої координатних чвертей.

Нехай функція y=f(u) є функція змінної u, визначеної на безлічі Uз областю значень Y, а змінна uу свою чергу є функцією u=φ (x), визначеної на безлічі Xз областю значень U. Тоді задана на безлічі Xфункція y=f(φ (x)) називається складною функцією(Композицією функцій, суперпозицією функцій, функцією від функції).

Елементарні функції

До основних елементарних функцій відносять:

• статечну функцію y=x n; y=x – nі y=x 1/ n;
• показову функцію y=a x;
• логарифмічну функцію y=log a x;
• тригонометричні функції y=sin x, y=cos x, y=tg xі y=ctg x;
• зворотні тригонометричні функції y= arcsin x, y=arccos x, y=arctg xі y= arcctg x.

З основних елементарних функцій нові функції можуть бути отримані за допомогою дій алгебри і суперпозицією функцій.

Функції, побудовані з основних елементарних функцій за допомогою кінцевого числа дій алгебри та кінцевого числа операцій суперпозиції, називаються елементарними.

Алгебраїчноїназивається функція, в якій над аргументом проводиться кінцеве число дій алгебри. До алгебраїчних функцій відносяться:

· Ціла раціональна функція (багаточлен або поліном)

· Дробально-раціональна функція (відношення двох багаточленів)

· Ірраціональна функція (якщо у складі операцій над аргументом є вилучення кореня).

Будь-яка неалгебраїчна функція називається трансцендентної. До трансцендентних функцій відносяться показова, логарифмічна, тригонометричні, зворотні тригонометричні функції.

Функції та їх властивості

Функція – одне з найважливіших математичних понять.функцією називають таку залежність змінної у від змінної х, за якої кожному значенню змінної х відповідає єдине значення змінної у.

Змінну хназивають незалежної змінної або аргументом.Змінну уназивають залежною змінною. Говорять також, щозмінна у є функцією від змінної х. Значення залежної змінної називаютьзначеннями функції.

Якщо залежність змінноїу від змінноїх є функцією, то коротко це записують так:y= f( x ). (Читають:у одноf відх .) Символомf( x) позначають значення функції, що відповідає значенню аргументу, що дорівнюєх .

Усі значення незалежної змінної утворюютьобласть визначення функції . Усі значення, які набуває залежна змінна, утворюютьобласть значень функції .

Якщо функція задана формулою та її область визначення не зазначена, то вважають, що область визначення функції складається з усіх значень аргументу, у яких формула має сенс.

Способи завдання функції:

1.аналітичний метод (функція задається з допомогою математичної формули;

2. табличний спосіб (функція задається за допомогою таблиці)

3.описовий спосіб (функція задається словесним описом)

4.графічний спосіб (функція задається з допомогою графіка).

Графіком функції називають безліч всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати - відповідним значенням функції.

ОСНОВНІ ВЛАСТИВОСТІ ФУНКЦІЙ

1. Нулі функції

Нуль функції - таке значення аргументу, при якому значення функції дорівнює нулю.

2. Проміжки знаковості функції

Проміжки знакостійності функції – такі безлічі значень аргументу, у яких значення функції лише позитивні чи лише негативні.

3. Зростання (зменшення) функції.

Зростаюча в деякому проміжку функція - функція, яка має більшому значенню аргументу з цього проміжку відповідає більше значення функції.

Функція у = f ( x ) називається зростаючою на інтервалі (А; b ), якщо для будь-яких x 1 і x 2 з цього інтервалу таких, щоx 1 < x 2 , справедлива нерівністьf ( x 1 )< f ( x 2 ).

Знижена в деякому проміжку функція - функція, яка має більшому значенню аргументу з цього проміжку відповідає менше значення функції.

Функція у = f ( x ) називається спадаючоюна інтервалі (А; b ) , якщо для будь-яких x 1 і x 2 з цього інтервалу таких, що x 1 < x 2 , справедлива нерівністьf ( x 1 )> f ( x 2 ).

4. Парність (непарність) функції

Парна функція - функція, у якої область визначення симетрична щодо початку координат та для будь-якогох в галузі визначення виконується рівністьf (- x ) = f ( x ) . Графік парної функції симетричний щодо осі ординат.

Наприклад, у = х 2 - парна функція.

Непарна функція- функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення справедлива рівність f (- x ) = - f (x ). Графік непарної функції симетричний щодо початку координат.

Наприклад: у = х 3 - непарна функція .

Функція загального вигляду не є парною або непарною (у = х 2 +х ).

Властивості деяких функцій та їх графіки

1. Лінійною функцією називається функція виду , де k і b - Числа.

Область визначення лінійної функції – безлічR дійсних чисел.

Графік лінійної функціїу = kx + b ( k ≠ 0) є пряма через точку (0;b ) і паралельна прямийу = kx .

Пряма, не паралельна осіОу, є графіком лінійної функції.

Властивості лінійної функції.

1. При k > 0 функція у = kx + b

2. При k < 0 функція у = kx + b спадна в області визначення.

y = kx + b ( k ≠ 0 ) є вся числова пряма, тобто. безлічR дійсних чисел.

При k = 0 безліч значень функціїу = kx + b складається з одного числаb .

3. При b = 0 і k = 0 функція не є ні парною, ні непарною.

При k = 0 лінійна функція має вигляду = b і при b ≠ 0 вона є парною.

При k = 0 і b = 0 лінійна функція має вигляду = 0 і виявляєте одночасно парною та непарною.

Графік лінійної функціїу = b є пряма, яка проходить через точку (0; b ) та паралельна осіОх.Зауважимо, що при b = 0 графік функціїу = b збігаєтеся віссю Ох .

5. При k > 0 маємо, що у> 0, якщо і у< 0, якщо . При k < 0 маємо, що у > 0, якщоі у< 0, если .

2. Функція y = x 2

Rдійсних чисел.

Надаючи змінноїх кілька значень з області визначення функції та обчислюючи відповідні значенняуза формулою y = x 2 , Зображаємо графік функції.

Графік функції y = x 2 називається параболою.

Властивості функції у = х 2 .

1. Якщо х= 0, то у = 0, тобто. парабола має з осями координат загальну точку (0; 0) – початок координат.

2. Якщо х ≠ 0 , то у > 0, тобто. всі точки параболи, крім початку координат, лежать над віссю абсцис.

3. Безліч значень функціїу = х 2 є проміжок функціяу = х 2 зменшується.

х

3.Фунуція

Область визначення цієї функції - проміжок функціїy = | x | зменшується.

7. Найменше значення функція набуває в точціх,воно одно 0. Найбільшого значенняне існує.

6. Функція

Область визначення функції: .

Область значень функції: .

Графік – гіпербола.

1. Нулі функції.

у ≠ 0, нулів немає.

2. Проміжки знакостійності,

Якщо k > 0, то у> 0 при х > 0; у < 0 при х < О.

Якщо k < 0, то у < 0 при х > 0; у> 0 при х < 0.

3. Проміжки зростання та спадання.

Якщо k > 0, то функція зменшується при .

Якщо k < 0, то функция возрастает при .

4. Парність (непарність) функції.

Функція непарна.

Квадратний тричлен

Рівняння виду ax 2 + bx + c = 0, де a , bі з - Деякі числа, причомуа≠ 0, називається квадратним.

У квадратному рівнянніax 2 + bx + c = 0 коефіцієнт аназивається першим коефіцієнтом, b - другим коефіцієнтам, з - вільним членом.

Формула коріння квадратного рівняннямає вигляд:

.

Вираз називається дискримінантом квадратного рівняння і позначається черезD .

Якщо D = 0, то існує лише одне число, що задовольняє рівняння ax 2 + bx + c = 0. Однак домовилися говорити, що в цьому випадку квадратне рівняння має два рівні дійсні корені, а саме число називають дворазовим коренем.

Якщо D < 0, то квадратное уравнение не имеет действительных корней.

Якщо D > 0, то квадратне рівняння має два різних дійсних кореня.

Нехай дано квадратне рівнянняax 2 + bx + c = 0. Так як а≠ 0, то, розділивши обидві частини даного рівняння наа, отримаємо рівняння . Вважаючи і , приходимо до рівняння , в якому перший коефіцієнт дорівнює 1. Таке рівняння називаєтьсянаведеним.

Формула коренів наведеного квадратного рівняння має вигляд:

.

Рівняння виду

а x 2 + bx = 0, ax 2 + с = 0, а x 2 = 0

називаються неповними квадратними рівняннями. Неповні квадратні рівняння розв'язуються розкладанням лівої частини рівняння на множники.

Теорема Вієта .

Сума коренів квадратного рівняння дорівнює взятому з протилежним знаком відношенню другого коефіцієнта першого, а добуток коренів - відношенню вільного члена першого коефіцієнта, тобто.

Зворотна теорема.

Якщо сума якихось двох чиселх 1 і х 2 дорівнює , А їх твір одно, то ці числа є корінням квадратного рівнянняах 2 + b х + с = 0.

Функція виду ах 2 + b х + сназивається квадратним тричленом. Коріння цієї функції є корінням відповідного квадратного рівнянняах 2 + b х + с = 0.

Якщо дискримінант квадратного тричленабільше за нуль, то цей тричлен можна представити у вигляді:

ах 2 + b х + с = а (х-х 1 )(х-х 2 )

де х 1 і х 2 - коріння тричлена

Якщо дискримінант квадратного тричлена дорівнює нулю, цей тричлен можна представити у вигляді:

ах 2 + b х + с = а (х-х 1 ) 2

де х 1 - Корінь тричлена.

Наприклад, 3х 2 - 12х + 12 = 3 (х - 2) 2 .

Рівняння виду ах 4 + b х 2 + с= 0 називається біквадратним. За допомогою заміни змінної за формулоюх 2 = y воно наводиться до квадратного рівнянняа y 2 + by + с = 0.

Квадратична функція

Квадратичною функцією називається функція, яку можна записати формулою видуy = ax 2 + bx + c , де x - незалежна змінна,a , b і c - Деякі числа, причомуa ≠ 0.

Властивості функції та вид її графіка визначаються в основному значеннями коефіцієнтаa та дискримінанта.

Властивості квадратичної функції

Область визначення:R;

Область значень:

при а > 0 [- D/(4 a); ∞)

при а < 0 (-∞; - D/(4 a)];

Парність, непарність:

при b = 0 функція парна

при b ≠ 0 функція не є ні парною, ні непарною

при D> 0 два нулі: ,

при D= 0 один нуль:

при D < 0 нулей нет

Проміжки знакостійності:

якщо, а > 0, D> 0, то

якщо, а > 0, D= 0, то

eякщо а > 0, D < 0, то

якщо а< 0, D> 0, то

якщо а< 0, D= 0, то

якщо а< 0, D < 0, то

- Проміжки монотонності

при а > 0

при а< 0

Графіком квадратичної функції єпарабола - крива, симетрична щодо прямої , що проходить через вершину параболи (вершиною параболи називається точка перетину параболи з віссю симетрії).

Щоб побудувати графік квадратичної функції, потрібно:

1) знайти координати вершини параболи та відзначити її в координатній площині;

2) побудувати ще кілька точок, що належать параболі;

3) з'єднати зазначені точки плавною лінією.

Координати вершини параболи визначаються за формулами:

; .

Перетворення графіків функції

1. Розтягування графікау = х 2 вздовж осіу в|а| раз (при|а| < 1 - це стиск в 1/|а| разів).

Якщо, а< 0, произвести, кроме того, зеркальное отражение графика отно­сительно оси х (Гілки параболи будуть спрямовані вниз).

Результат: графік функціїу = ах 2 .

2. Паралельне перенесення графіка функціїу = ах 2 вздовж осіх на| m | (вправо при

m > 0 і вліво прит< 0).

Результат: графік функціїу = а(х - т) 2 .

3. Паралельне перенесення графіка функції вздовж осіу на| n | (вгору прип > 0 і вниз прип< 0).

Результат: графік функціїу = а(х - т) 2 + п.

Квадратичні нерівності

Нерівності видуах 2 + b х + с > 0 таах 2 + bх + с< 0, дех - змінна,a , b із - Деякі числа, причому,а≠ 0 називають нерівностями другого ступеня з однією змінною.

Вирішення нерівності другого ступеня з однією змінною можна розглядати як знаходження проміжків, у яких відповідна квадратична функція набуває позитивних або негативних значень.

Для вирішення нерівностей видуах 2 + bх + с > 0 таах 2 + bх + с< 0 надходять таким чином:

1) знаходять дискримінант квадратного тричлена та з'ясовують, чи має тричлен коріння;

2) якщо тричлен має коріння, то відзначають їх на осіх і через зазначені точки проводять схематично параболу, гілки якої спрямовані вгору приа > 0 або вниз приа< 0; якщо тричлен не має коріння, то схематично зображують параболу, розташовану у верхній напівплощині приа > 0 або в нижній приа < 0;

3) знаходять на осіх проміжки, для яких точки параболи розташовані вище осіх (якщо вирішують нерівністьах 2 + bх + с > 0) або нижче осіх (якщо вирішують нерівністьах 2 + bх + с < 0).

Приклад:

Розв'яжемо нерівність .

Розглянемо функцію

Її графіком є ​​парабола, гілки якої спрямовані вниз (т.к. ).

З'ясуємо, як розташований графік щодо осіх. Вирішимо для цього рівняння . Отримаємо, щох = 4. Рівняння має єдине коріння. Значить, парабола стосується осіх.

Зобразивши схематично параболу, знайдемо, що функція набуває негативних значень при будь-якомух, крім 4.

Відповідь можна записати так:х - будь-яке число, що не дорівнює 4.

Розв'язання нерівностей методом інтервалів

схема рішення

1. Знайти нулі функції, що стоїть у лівій частині нерівності.

2. Відзначити положення нулів на числовій осі та визначити їхню кратність (якщоk i парне, то нуль парної кратності, якщоk i непарне - то непарне).

3. Знайти знаки функції у проміжках між її нулями, починаючи з крайнього правого проміжку: у цьому проміжку функція у лівій частині нерівності завжди позитивна для наведеного виду нерівностей. При переході праворуч наліво через нуль функції від одного проміжку до сусіднього слід враховувати:

якщо нуль непарний кратності, знак функції змінюється,

якщо нуль парний кратність, знак функції зберігається.

4. Записати відповідь.

Приклад:

(х + 6) (х + 1) (х - 4) < 0.

Знайдено нулі функції. Вони рівні:х 1 = -6; х 2 = -1; х 3 = 4.

Зазначимо на координатній прямій нулі функціїf ( x ) = (х + 6) (х + 1) (х - 4).

Знайдемо знаки цієї функції у кожному з проміжків (-∞; -6), (-6; -1), (-1; 4) та

З малюнка видно, що множиною розв'язків нерівності є об'єднання проміжків (-∞; -6) і (-1; 4).

Відповідь: (-∞ ; -6) та (-1; 4).

Розглянутий спосіб розв'язання нерівностей називаютьметодом інтервалів.

Даний методичний матеріалносить довідковий характер і належить до широкого кола тем. У статті наведено огляд графіків основних елементарних функцій та розглянуто найважливіше питання – як правильно і ШВИДКО побудувати графік. У ході вивчення вищої математики без знання графіків основних елементарних функцій доведеться важко, тому дуже важливо згадати, як виглядають графіки параболи, гіперболи, синуси, косинуси і т.д., запам'ятати деякі значення функцій. Також мова піде про деякі властивості основних функцій.

Я не претендую на повноту та наукову обґрунтованість матеріалів, наголос буде зроблено, перш за все, на практиці – тих речах, з якими доводиться стикатися буквально на кожному кроці, у будь-якій темі вищої математики. Графіки для чайників? Можна сказати і так.

На численні прохання читачів клікабельний зміст:

Крім того, є надкороткий конспект на тему
– освойте 16 видів графіків, вивчивши шість сторінок!

Серйозно, шість, здивувався навіть сам. Даний конспект містить покращену графіку і доступний за символічну плату, демо-версію можна переглянути. Файл зручно надрукувати, щоб графіки завжди були під рукою. Дякуємо за підтримку проекту!

І одразу починаємо:

Як правильно збудувати координатні осі?

Насправді контрольні роботи майже завжди оформляються студентами у окремих зошитах, розлинованих у клітину. Навіщо потрібна картата розмітка? Адже роботу, загалом, можна зробити і на листах А4. А клітина необхідна саме для якісного та точного оформлення креслень.

Будь-яке креслення графіка функції починається з координатних осей.

Креслення бувають двомірними та тривимірними.

Спочатку розглянемо двовимірний випадок декартової прямокутної системи координат:

1) Чортимо координатні осі. Вісь називається віссю абсцис , а вісь – віссю ординат . Рисувати їх завжди намагаємося акуратно і не криво. Стрілки теж не повинні нагадувати бороду Папи Карло.

2) Підписуємо осі великими літерами «ікс» та «ігрок». Не забуваємо підписувати осі.

3) Задаємо масштаб по осях: малюємо нуль і дві одиниці. При виконанні креслення найзручніший і найпоширеніший масштаб: 1 одиниця = 2 клітинки (креслення зліва) – по можливості дотримуйтеся саме його. Однак іноді трапляється так, що креслення не вміщається на зошит - тоді масштаб зменшуємо: 1 одиниця = 1 клітинка (креслення праворуч). Рідко, але буває, що масштаб креслення доводиться зменшувати (чи збільшувати) ще більше

НЕ ТРЕБА «строчити з кулемета» …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, ….Бо координатна площина– не пам'ятник Декарту, а студент – не голуб. Ставимо нульі дві одиниці по осях. Іноді замістьодиниць зручно "засікти" інші значення, наприклад, "двійку" на осі абсцис і "трійку" на осі ординат - і ця система (0, 2 і 3) теж однозначно задасть координатну сітку.

Передбачувані розміри креслення краще оцінити ще до побудови креслення. Так, наприклад, якщо в завдання потрібно накреслити трикутник з вершинами , , , то цілком зрозуміло, що популярний масштаб 1 одиниця = 2 клітинки не підійде. Чому? Подивимося на точку - тут доведеться відміряти п'ятнадцять сантиметрів вниз, і, очевидно, що креслення не вмоститься (або вмоститься ледве) на зошит. Тому одночасно вибираємо дрібніший масштаб 1 одиниця = 1 клітинка.

До речі, про сантиметри і зошити. Чи правда, що у 30 зошитових клітинах міститься 15 сантиметрів? Відміряйте у зошиті для інтересу 15 сантиметрів лінійкою. В СРСР, можливо, це було правдою… Цікаво відзначити, що якщо відміряти ці сантиметри по горизонталі та вертикалі, то результати (у клітинах) будуть різними! Строго кажучи, сучасні зошити не картаті, а прямокутні. Можливо, це здасться нісенітницею, але, креслити, наприклад, коло циркулем при таких розкладах дуже незручно. Якщо чесно, в такі моменти починаєш замислюватися про правоту товариша Сталіна, який відправляв у табори за халтуру на виробництві, не кажучи вже про вітчизняне автомобілебудування, літаки, що вибухають, або вибухові електростанції.

До речі про якість, або коротка рекомендація щодо канцтоварів. Сьогодні більшість зошитів у продажу, поганих слів не кажучи, повне гомно. Тому, що вони промокають, причому не тільки від гелевих, а й від кулькових ручок! На папері заощаджують. Для оформлення контрольних робітрекомендую використовувати зошити Архангельського ЦПК (18 аркушів, клітина) або «П'ятірку», щоправда, вона дорожча. Ручку бажано вибрати гелеву, навіть найдешевший китайський гелевий стрижень набагато краще, ніж кулькова ручка, яка то маже, то б'є папір. Єдиною «конкурентоспроможною» кульковою ручкоюна моїй пам'яті є "Еріх Краузе". Вона пише чітко, красиво та стабільно – що з повним стрижнем, що із практично порожнім.

Додатково: бачення прямокутної системи координат очима аналітичної геометрії висвітлюється у статті Лінійна (не) залежність векторів. Базис векторів, детальну інформацію про координатні чверті можна знайти у другому параграфі уроку Лінійні нерівності.

Тривимірний випадок

Тут майже так само.

1) Чортимо координатні осі. Стандарт: вісь аплікат – спрямована вгору, вісь – спрямована вправо, вісь – ліворуч вниз суворопід кутом 45 градусів.

2) Підписуємо осі.

3) Задаємо масштаб по осях. Масштаб по осі – вдвічі менше, ніж масштаб по інших осях. Також зверніть увагу, що на правому кресленні я використав нестандартну «засічку» по осі (про таку можливість вже згадано вище). На мій погляд, так точніше, швидше і естетичніше – не потрібно під мікроскопом вишукувати середину клітини і «ліпити» одиницю впритул до початку координат.

При виконанні тривимірного креслення знову ж таки – віддавайте пріоритет масштабу
1 одиниця = 2 клітини (креслення зліва).

Навіщо потрібні всі ці правила? Правила є для того, щоб їх порушувати. Чим я зараз і займусь. Справа в тому, що наступні креслення статті будуть виконані мною в Екселе, і координатні осі будуть виглядати некоректно з точки зору правильного оформлення. Я міг би накреслити всі графіки від руки, але креслити їх насправді жах як небажання Ексель їх накреслить набагато точніше.

Графіки та основні властивості елементарних функцій

Лінійна функція задається рівнянням. Графік лінійної функцій є пряму. Для того, щоб побудувати пряму, достатньо знати дві точки.

Приклад 1

Побудувати графік функції. Знайдемо дві точки. Як одну з точок вигідно вибрати нуль.

Якщо то

Беремо ще якусь точку, наприклад, 1.

Якщо то

При оформленні завдань координати точок зазвичай зводяться до таблиці:

А самі значення розраховуються усно чи на чернетці, калькуляторі.

Дві точки знайдені, виконаємо креслення:

При оформленні креслення завжди підписуємо графіки.

Не зайвим буде згадати окремі випадки лінійної функції:

Зверніть увагу, як я розташував підписи, підписи не повинні допускати різночитань щодо креслення. У разі вкрай небажано було поставити підпис поруч із точкою перетину прямих , чи праворуч унизу між графіками.

1) Лінійна функція виду () називається прямою пропорційністю. Наприклад, . Графік прямої пропорційності завжди проходить через початок координат. Таким чином, побудова прямої спрощується - достатньо знайти лише одну точку.

2) Рівняння виду задає пряму, паралельну осі, зокрема, сама вісь задається рівнянням. Графік функції будується відразу, без будь-яких точок. Тобто запис слід розуміти так: «гравець завжди дорівнює -4, при будь-якому значенні ікс».

3) Рівняння виду задає пряму, паралельну осі, зокрема, сама вісь задається рівнянням. Графік функції також будується одразу. Запис слід розуміти так: «ікс завжди, за будь-якого значення ігор, дорівнює 1».

Дехто запитає, ну навіщо згадувати 6 клас?! Так-то воно, може і так, тільки за роки практики я зустрів добрий десяток студентів, яких ставило в глухий кут завдання побудови графіка на кшталт або .

Побудова прямий – найпоширеніша дія у виконанні креслень.

Пряма лінія детально розглядається в курсі аналітичної геометрії, і бажаючі можуть звернутись до статті Рівняння прямої на площині.

Графік квадратичної, кубічної функції, графік багаточлена

Парабола. Графік квадратичної функції () являє собою параболу. Розглянемо знаменитий випадок:

Згадуємо деякі властивості функції.

Отже, рішення нашого рівняння: - Саме в цій точці і знаходиться вершина параболи. Чому це так, можна дізнатися з теоретичної статті про похідну та уроку про екстремуми функції . А поки що розраховуємо відповідне значення «гравець»:

Таким чином, вершина знаходиться в точці

Тепер знаходимо інші точки, при цьому нахабно користуємося симетричністю параболи. Слід зауважити, що функція – не є парноюПроте, симетричність параболи ніхто не скасовував.

В якому порядку знаходити інші точки, гадаю, буде зрозуміло з підсумкової таблиці:

Даний алгоритм побудови образно можна назвати "човником" або принципом "туди-сюди" з Анфісою Чеховою.

Виконаємо креслення:

З розглянутих графіків згадується ще одна корисна ознака:

Для квадратичної функції () справедливо наступне:

Якщо , то гілки параболи спрямовані нагору.

Якщо , то гілки параболи спрямовані вниз.

Поглиблені знання про криву можна отримати на уроці гіпербола і парабола.

Кубічна парабола задається функцією. Ось знайоме зі школи креслення:

Перерахуємо основні властивості функції

Графік функції

Він є однією з гілок параболи. Виконаємо креслення:

Основні властивості функції:

В даному випадку вісь є вертикальною асимптотою для графіка гіперболи при .

Буде ГРУБИЙ помилкою, якщо при оформленні креслення з недбалості допустити перетин графіка з асимптотою .

Також односторонні межі говорять нам про те, що гіпербола не обмежена зверхуі не обмежена знизу.

Досліджуємо функцію на нескінченності: тобто якщо ми почнемо йти по осі вліво (або вправо) на нескінченність, то «ігреки» струнким кроком будуть нескінченно близьконаближатися до нуля, і, відповідно, гілки гіперболи нескінченно близьконаближатися до осі.

Таким чином, вісь є горизонтальною асимптотою для графіка функції, якщо «ікс» прагне плюс або мінус нескінченності.

Функція є непарний, отже, гіпербола симетрична щодо початку координат. Цей факт очевидний з креслення, крім того, легко перевіряється аналітично: .

Графік функції виду () являє собою дві гілки гіперболи.

Якщо , то гіпербола розташована в першій та третій координатних чвертях(Див. малюнок вище).

Якщо , то гіпербола розташована у другій та четвертій координатних чвертях.

Зазначену закономірність місця проживання гіперболи неважко проаналізувати з погляду геометричних перетворень графіків.

Приклад 3

Побудувати праву гілку гіперболи

Використовуємо поточковий метод побудови, при цьому значення вигідно підбирати так, щоб ділилося націло:

Виконаємо креслення:

Не важко побудувати і ліву гілку гіперболи, тут якраз допоможе непарність функції. Грубо кажучи, в таблиці поточкового побудови подумки додаємо до кожного мінус, ставимо відповідні точки і прокреслюємо другу гілку.

Детальну геометричну інформацію про розглянуту лінію можна знайти у статті Гіперболу та параболу.

Графік показової функції

У даному параграфі я одразу розгляну експоненційну функцію, оскільки у завданнях вищої математики у 95% випадків зустрічається саме експонента.

Нагадую, що – це ірраціональне число: це буде потрібно при побудові графіка, який, власне, я без церемоній і побудую. Трьох точок, мабуть, вистачить:

Графік функції поки дамо спокій, про нього пізніше.

Основні властивості функції:

Принципово так само виглядають графіки функцій, і т.д.

Повинен сказати, що другий випадок зустрічається на практиці рідше, але він зустрічається, тому я вважав за потрібне включити його до цієї статті.

Графік логарифмічної функції

Розглянемо функцію з натуральним логарифмом.
Виконаємо крапковий креслення:

Якщо забули, що таке логарифм, будь ласка, зверніться до шкільних підручників.

Основні властивості функції:

Область визначення:

Область значень: .

Функція не обмежена зверху: , Нехай і повільно, але гілка логарифму йде на нескінченність.
Досліджуємо поведінку функції поблизу нуля праворуч: . Таким чином, вісь є вертикальною асимптотою для графіка функції при "ікс", що прагне до нуля праворуч.

Обов'язково потрібно знати та пам'ятати типове значення логарифму: .

Принципово так само виглядає графік логарифму на підставі: , , (десятковий логарифм на підставі 10) і т.д. При цьому, що більша підстава, то більш пологім буде графік.

Випадок розглядати не будемо, щось я не пригадаю, коли востаннє будував графік із такою підставою. Та й логарифм начебто в завданнях вищої математики дуже рідкісний гість.

На закінчення параграфа скажу ще про один факт: Експоненційна функція та логарифмічна функція– це дві взаємно зворотні функції. Якщо придивитися до графіка логарифму, то можна побачити, що це - та сама експонента, просто вона розташована трохи по-іншому.

Графіки тригонометричних функцій

З чого починаються тригонометричні муки у школі? Правильно. З синуса

Побудуємо графік функції

Ця лінія називається синусоїдою.

Нагадую, що «пі» – це ірраціональне число: і в тригонометрії від нього в очах рябить.

Основні властивості функції:

Ця функція є періодичноїз періодом. Що це означає? Подивимося на відрізок. Зліва і праворуч від нього нескінченно повторюється такий самий шматок графіка.

Область визначення: , тобто для будь-якого значення ікс існує значення синуса.

Область значень: . Функція є обмеженою: тобто всі «ігреки» сидять строго у відрізку.
Такого немає: чи , точніше кажучи, буває, але зазначені рівняння немає рішення.